Circles, Polar Forms, and Roots in the Complex Plane

When the world says, ‘Give up,’ hope whispers, ‘Try it one more time’, Lyndon B. Johnson

Circle Equation in the Complex Plane

The equation |z - a| = r defines a circle in the complex plane where the distance between any point z on the circle and the center a is equal to the radius r. Components:

• z = x + iy represents any point on the circle
• a = h + ki is the center of the circle
• r is the radius of the circle, a positive real number.

Connection to Cartesian Form

The absolute value |z - a| represents the Euclidean distance between points z and a in the complex plane. This distance formula is: |z - a| = |x + yi - (h + ki)| = |(x - h) + (y - k)i| = $\sqrt{(x - h)² + (y - k)²}$

Setting this equal to $r$: $\sqrt{(x - h)^2 + (y - k)^2} = r$. Then, squaring both sides, we get the familiar Cartesian equation of a circle! $\boxed{(x - h)^2 + (y - k)^2 = r^2}$

Special Cases

• Circle centered at origin $a = (0, 0)$: $x^2 + y^2 = r^2$. This represents all complex numbers with magnitude (or modulus) r. It forms a circle of radius r centered at the origin, e.g., the unit circle, |z| = 1.
• Circle centered on real axis. Center a is real, a = (h, 0), $a \in \mathbb{R}: |z - h| = r, (x - h)^2 + y^2 = r^2$ where a = h ∈ ℝ.
• Circle centered on imaginary axis. Center a = (0, k) is purely imaginary: $|z - ki| = r, x^2 + (y - k)^2 = r^2 \quad \text{where } h \in \mathbb{R}$ and a = ki.

Regions Defined by Circle Inequalities

Inequality	Region	Description
$\vert z - a\vert < r$	Open disk	Interior of circle (excluding boundary)
$\vert z - a\vert \leq r$	Closed disk	Interior plus boundary
$\vert z - a\vert > r$	Exterior	Outside the circle
$\vert z - a\vert \geq r$	Closed exterior	Outside plus boundary
$\vert z - a\vert = r$	Circle	Boundary only

Annular regions

Notation	Region
$r_1 < \vert z - a\vert < r_2$ where $0 < r_1 < r_2$	Open annulus (ring-shaped region) centered at a
$r_1 ≤ \vert z - a\vert ≤ r_2$	Closed annulus
$r_1 < \vert z - a\vert≤ r_2$	Half-open annulus
$0 < \vert z - a\vert < r$	Punctured disk (center removed)
$\vert z - a\vert > r$	Exterior of disk

Half-Planes

Lines in the complex plane can be written as: $\Re(\bar{a}z) = c \quad \text{or} \quad \Im(\bar{a}z) = c$ with $a \in \mathbb{C} \setminus \{ 0 \}$ and $c \in \mathbb{R}$

Write a = u + iv (where u, v are real numbers) and z = x + iy (where x, y are real coordinates). Then, $\overline{a}z = (u -iv)(x +iy)=(ux +vy) +i(uy -vx)$.

In analytic geometry, a line in a 2D plane is defined by the equation: Ax + By = C where (A, B) is the normal vector (a vector perpendicular to the line).

• Case 1. $\Re(\overline{a}z) = ux + vy = c$ is the real linear equation of a line with normal vector a = (u, v). It describes a line perpendicular to the vector a (line ⊥ a).
• $\Im (\overline{a} z)= uy - vx = c \iff (-v)x + (u)y = c$ is the real linear equation with normal vector (-v, u) (a $90^{\circ}$ rotation of (u, v)).

  If you have a vector (u, v), rotating it 90∘ counter-clockwise swaps the components and negates the first one.

Half-planes

Inequality	Region
$\Re(z) > 0$	Right half-plane
$\Re(z) < 0$	Left half-plane
$\Im(z) > 0$	Upper half-plane
$\Im(z) < 0$	Lower half-plane

Product of Complex Numbers in Polar Form

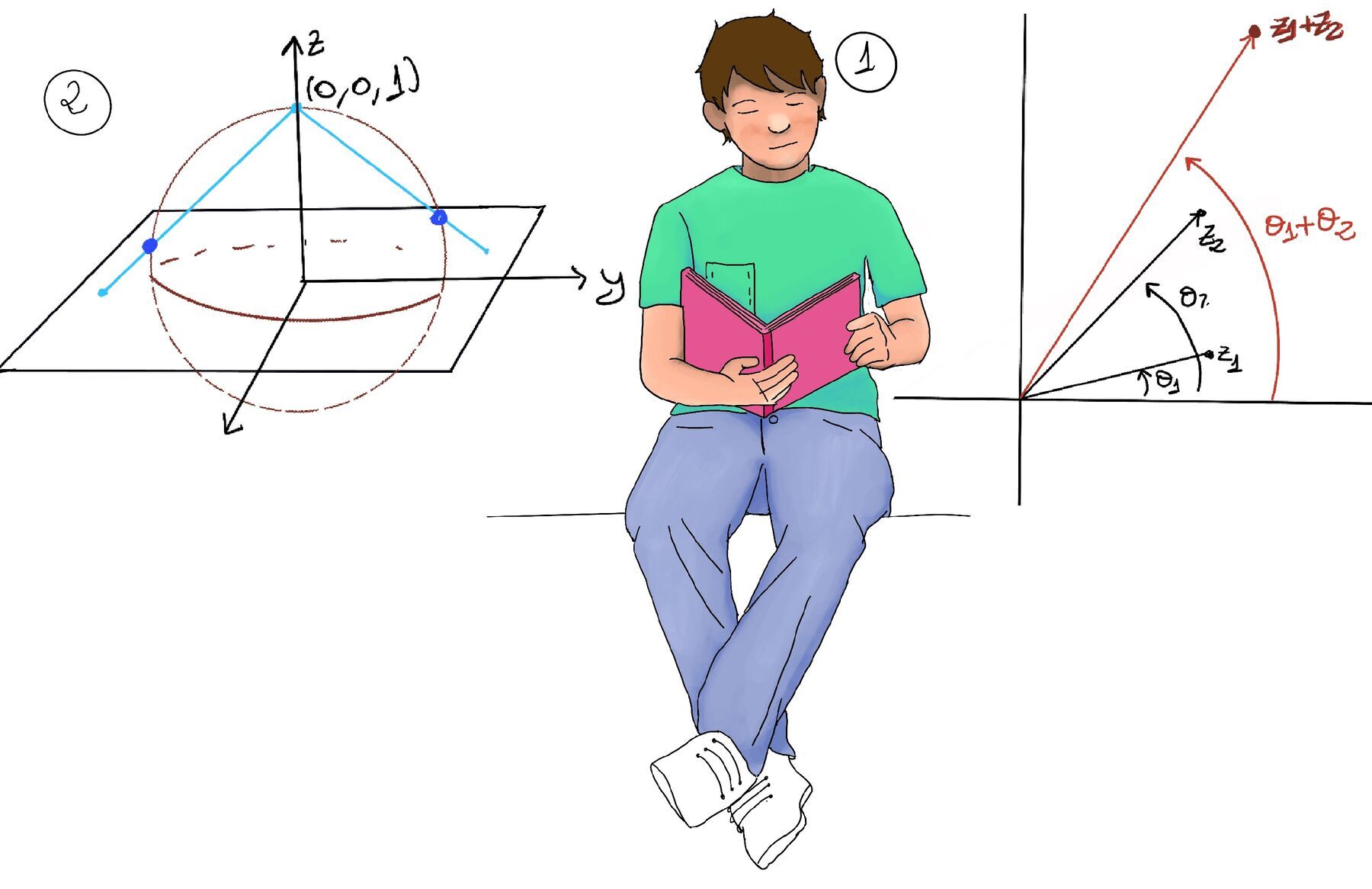
Let two complex numbers be given in polar form: $z_1 = r_1(cos(\theta_1) + isin(\theta_1)), z_2 = r_2(cos(\theta_2) + isin(\theta_2))$.

Derivation of Product Formula.

$$ \begin{aligned} z_1 \cdot z_2 &=r_1(\cos\theta_1 + i\sin\theta_1) \cdot r_2(\cos\theta_2 + i\sin\theta_2) \\[2pt] &= r_1 r_2 [(\cos\theta_1 + i\sin\theta_1)(\cos\theta_2 + i\sin\theta_2)] \\[2pt] &=[\text{Expanding}]r_1 r_2 [\cos\theta_1\cos\theta_2 + i\cos\theta_1\sin\theta_2 + i\sin\theta_1\cos\theta_2 + i^2\sin\theta_1\sin\theta_2] \\[2pt] &= r_1 r_2 [(\cos\theta_1\cos\theta_2 - \sin\theta_1\sin\theta_2) + i(\sin\theta_1\cos\theta_2 + \cos\theta_1\sin\theta_2)] \\[2pt] &\text{Using the angle addition formulas:} \cos(\alpha + \beta) = \cos\alpha\cos\beta - \sin\alpha\sin\beta, \sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta \\[2pt] &= r_1 r_2 [\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)] \end{aligned} $$

$\boxed{z_1 \cdot z_2 = r_1 r_2 [\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)]}$

The Multiplication Rules:

• Modulus: $|z_1||z_2| = r_1r_2$
• Argument: $arg(z_1·z_2) = \theta_1 + \theta_2 = arg(z_1)+arg(z_2)$.
• In words, the modulus of the product is the product of the moduli and the argument of the product is the sum of the arguments (Figure 1).
• In exponential form, this is immediate: $z_1 z_2 = r_1 e^{i\theta_1} \cdot r_2 e^{i\theta_2} = r_1 r_2 e^{i(\theta_1 + \theta_2)}$
• Geometric Interpretation: Multiplying a complex number $z_1$ by $z_2 = r_2 e^{i\theta_2}$ scales by a factor $r_2$ (stretches if $r_2 > 1$, shrinks if $r_2 < 1$) and rotates counterclockwise by angle $\theta_2$.
• Example: Multiply $z_1 = 2(\cos 30° + i\sin 30°)$ and $z_2 = 3(\cos 45° + i\sin 45°)$. $z_1 z_2 = 2 \cdot 3 [\cos(30° + 45°) + i\sin(30° + 45°)] = 6(\cos 75° + i\sin 75°)$

Division in Polar Form

$\frac{z_1}{z_2} = \frac{r_1 e^{i\theta_1}}{r_2 e^{i\theta_2}} = \frac{r_1}{r_2} e^{i(\theta_1 - \theta_2)}$

The Division Rules:

• Modulus: $\left \vert \frac{z_1}{z_2}\right \vert = \frac{\vert z_1 \vert}{\vert z_2 \vert}$
• Argument: $\arg\left(\frac{z_1}{z_2}\right) = \arg(z_1) - \arg(z_2)$

De Moivre’s Theorem

De Moivre’s Theorem: For any complex number $z = r(\cos\theta + i\sin\theta)$ and any $n$: $\boxed{z^n = r^n(\cos(n\theta) + i\sin(n\theta))}, \boxed{(\cos\theta + i\sin\theta)^n = \cos(n\theta) + i\sin(n\theta)}$. Or in exponential notation: $\boxed{(e^{i\theta})^n = e^{in\theta}}$

Proof by Induction

Base Cases: It is obviously a true statement for n = 0 ($z^0 = 1 = r^0(cos(0) + isin(0))$) and 1 ($z^1 = r(\cos\theta + i\sin\theta) = r^1(\cos(1 \cdot \theta) + i\sin(1 \cdot \theta)) \quad \checkmark$).

Inductive step: Assume the theorem holds for n = k, $z^k = r^k(\cos(k\theta) + i\sin(k\theta))$. We aim to prove it for n = k + 1.

$$ \begin{aligned} z^{k+1} &=z^k \cdot z \\[2pt] &\text{Inductive step, n = k} \\[2pt] &=r^k(\cos(k\theta) + i\sin(k\theta)) \cdot r(\cos\theta + i\sin\theta) \\[2pt] &=r^{k+1}[(\cos(k\theta)\cos\theta - \sin(k\theta)\sin\theta) + i(\cos(k\theta)\sin\theta + \sin(k\theta)\cos\theta)]\\[2pt] &\text{Using angle addition formulas: sin(α + β) = sin α cos β + cos α sin β and cos(α + β) = cos α cos β - sin α sin β} \\[2pt] &= r^{k+1}[\cos((k+1)\theta) + i\sin((k+1)\theta)] \quad \blacksquare \end{aligned} $$

Extension to Negative Integer. For n = -1:

$$ \begin{aligned} z^{-1} = \frac{1}{z} &=\frac{1}{r(\cos\theta + i\sin\theta)}\\[2pt] &\text{[Multiply by conjugate:]} =\frac{1}{r} \cdot \frac{\cos\theta - i\sin\theta}{(\cos\theta + i\sin\theta)(\cos\theta - i\sin\theta)} \\[2pt] &= \frac{1}{r} \cdot \frac{\cos\theta - i\sin\theta}{\cos^2\theta + \sin^2\theta} \\[2pt] &= \frac{1}{r}(\cos\theta - i\sin\theta) = r^{-1}(\cos(-\theta) + i\sin(-\theta)) \quad \checkmark \end{aligned} $$

For general negative $n = -m$ (where $m > 0$):

$$ \begin{aligned} z^{-m} &=(z^m)^{-1} \\[2pt] &[\text{By previous demonstration, the equality holds }] \\[2pt] &=\frac{1}{r^m(\cos(m\theta) + i\sin(m\theta))} \\[2pt] &=\frac{1}{r^m(\cos(m\theta) + i\sin(m\theta))}\frac{\cos(m\theta) - i\sin(m\theta)}{\cos(m\theta) - i\sin(m\theta)} = r^{-m}(\frac{\cos(m\theta) - i\sin(m\theta)}{\cos^2(m\theta) + \sin^2(m\theta)}) \\[2pt] &= r^{-m}(\cos(-m\theta) + i\sin(-m\theta)) \quad \checkmark \end{aligned} $$

De Moivre's Theorem. $z^n = r^n(cos(n\theta)+isin(n\theta))$ and the equality holds $\forall n \in \mathbb{Z}.$

Alternative Proof Using Euler’s Formula: $(\cos\theta + i\sin\theta)^n =[\text{Euler's formula}] (e^{i\theta})^n =[\text{Exponential law: } (e^a)^n = e^{an}] e^{in\theta} = \cos(n\theta) + i\sin(n\theta) \quad \blacksquare$

N-th Roots of a Complex Number

Given $z = re^{i\theta}$, find all $w$ such that $w^n = z$. General Solution: $\boxed{w_k = r^{1/n} e^{i(\theta + 2\pi k)/n} = \sqrt[n]{r}\left(\cos\frac{\theta + 2\pi k}{n} + i\sin\frac{\theta + 2\pi k}{n}\right)}$ for $k = 0, 1, 2, \ldots, n-1$

There are exactly $n$ distinct roots, one for each k = 0, 1, …, n-1. All roots have the same modulus $\vert w_k\vert \ = \sqrt[n]{r} = \vert z \vert^{1/n}$. Consecutive roots’ arguments differ by $\frac{2\pi}{n}$ radians, so they lie on a circle of radius $\sqrt[n]{r}$ centered at the origin and form the vertices of a regular n-gon. If $\theta = Arg(z)$, then the principal n-th root is $w_0 = \sqrt[n]{r} e^{i\theta/n}$ (when $\theta = \text{Arg}(z)$) and the other roots are obtained by successively adding $\frac{2\pi}{n}$ to its argument.

If $z \ne 0$ and we write it in polar form as $z = |z| e^{iArg(z)}$, then all the $n$-th roots of $z$ can be written as: $\boxed{w_k = \sqrt[n]{z} \cdot \omega_n^k}$, k = 0, 1, …, n- 1 where:

• $\sqrt[n]{z} = \sqrt[n]{|z|} e^{i\text{Arg}(z)/n}$ is the principal $n$-th root
• $\omega_n = e^{2\pi i/n}$ is the primitive $n$-th root of unity
• Geometrically intuition: you take the principal n-th root ($\sqrt[n]{z} = \sqrt[n]{|z|} e^{i\text{Arg}(z)/n}$) and rotate it successively by angles 2π/n around the origin to get the remaining roots, which form a regular n-gon on the circle of radius.

Find all fourth roots of $z = -3$.

1. Write or express it in polar form: $-3 = 3 \cdot e^{i\pi} = 3(\cos\pi + i\sin\pi)$. More generally, accounting for periodicity: $-3 = 3e^{i(\pi + 2\pi k)} \quad \text{for any integer } k$
2. Apply the root formula: $w = (-3)^{1/4} = 3^{1/4} e^{i(\pi + 2\pi k)/4} = \sqrt[4]{3}\left(\cos\frac{\pi + 2\pi k}{4} + i\sin\frac{\pi + 2\pi k}{4}\right)$
3. Calculate for $k = 0, 1, 2, 3$: (i) k = 0, $\sqrt[4]{3}\left(\frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2}\right) = \frac{\sqrt[4]{3}}{\sqrt{2}}(1 + i);$ (ii) k = 1, $\sqrt[4]{3}\left(-\frac{\sqrt{2}}{2} + i\frac{\sqrt{2}}{2}\right) = \frac{\sqrt[4]{3}}{\sqrt{2}}(-1 + i)$; (iii) k = 2, $\sqrt[4]{3}\left(-\frac{\sqrt{2}}{2} - i\frac{\sqrt{2}}{2}\right) = \frac{\sqrt[4]{3}}{\sqrt{2}}(-1 - i)$; (iv) k = 3, $\sqrt[4]{3}\left(\frac{\sqrt{2}}{2} - i\frac{\sqrt{2}}{2}\right) = \frac{\sqrt[4]{3}}{\sqrt{2}}(1 - i)$
4. Conclusion: $w = \sqrt[4]{3}\left(\pm\frac{1}{\sqrt{2}} \pm \frac{i}{\sqrt{2}}\right) = \frac{\sqrt[4]{3}}{\sqrt{2}}(\pm 1 \pm i)$