Derivate of Exponential and Logarithms

A learning experience is one of those things that says, ‘You know that thing you just did? Don’t do that, Douglas Adams

Recall

The derivative of a function at a specific input value describes the instantaneous rate of change. Geometrically, when the derivative exists, it is the slope of the tangent line to the graph of the function at that point. Algebraically, it represents the ratio of the change in the dependent variable to the change in the independent variable as the change approaches zero.

Definition. A function f(x) is differentiable at a point “a” in its domain, if its domain contains an open interval around “a”, and the following limit exists $f'(a) = L = \lim _{h \to 0}{\frac {f(a+h)-f(a)}{h}}$. More formally, for every positive real number ε, there exists a positive real number δ, such that for every h satisfying 0 < |h| < δ, then the following inequality holds |L-$\frac {f(a+h)-f(a)}{h}$|< ε.

Basic important derivatives

1. Power Rule: $\frac{d}{dx}(x^n) = nx^{n-1}$ (works for any real n).
2. Sum Rule: $\frac{d}{dx}(f(x) + g(x)) = \frac{d}{dx}(f(x)) + \frac{d}{dx}(g(x))$
3. Difference Rule: $\frac{d}{dx}(f(x) - g(x)) = f'(x) - g'(x)$
4. Constant Multiple Rule: $\frac{d}{dx}(c \cdot f(x)) = c \cdot f'(x)$ where c is a constant.
5. Product Rule: $\frac{d}{dx}(f(x) \cdot g(x)) = f'(x)g(x) + f(x)g'(x)$.
6. Quotient Rule: $\frac{d}{dx}\left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x) - f(x)g'(x)}{(g(x))^2}$, provided $g(x) \ne 0$.
7. Chain Rule: $\frac{d}{dx}(f(g(x))) = f'(g(x)) \cdot g'(x)$

Common Derivatives

1. Exponential & Logarithmic: $\frac{d}{dx}(e^x) = e^x, \frac{d}{dx}(\ln(x)) = \frac{1}{x}$ for x > 0, $\frac{d}{dx}(a^x) = a^x \ln(a)$ for a > 0, $\frac{d}{dx}(log_a x) = \frac{1}{xln(a)}$.
2. Trigonometric: $\frac{d}{dx}(\sin(x)) = \cos(x), \frac{d}{dx}(\cos(x)) = -\sin(x), \frac{d}{dx}(\tan(x)) = \sec^2(x)$, $\frac{d}{dx}(\csc(x)) = -\csc(x) \cot(x), \frac{d}{dx}(\sec (x)) = \sec(x)\tan(x),\frac{d}{dx}(\cot(x)) = -\csc^2(x).$
3. Inverse Trigonometric: $\frac{d}{dx}(\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}}$ for |x| < 1, $\frac{d}{dx}(\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}}$, for |x| < 1, $\frac{d}{dx}(\arctan(x)) = \frac{1}{1 + x^2}, \frac{d}{dx}(arccsc(x)) = -\frac{1}{|x|\sqrt{x^2-1}}$ for |x| > 1, $\frac{d}{dx}(arcsec(x)) = \frac{1}{|x|\sqrt{x^2-1}}$ for |x| > 1, $\frac{d}{dx}(arccot(x)) = -\frac{1}{1 + x^2}$.

Derivate of Exponential and Logarithms functions.

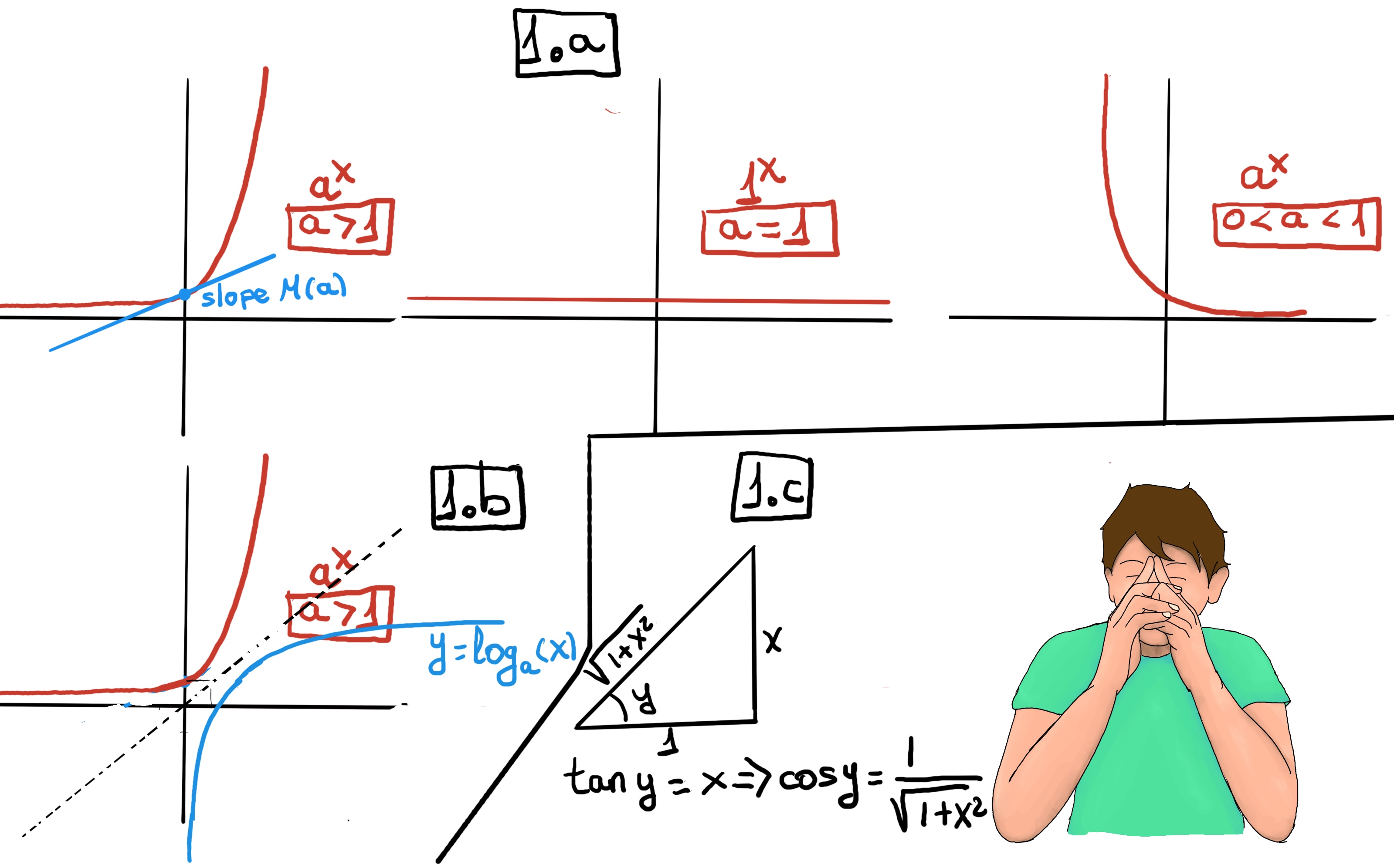
An exponential function is a function of the form f(x) = a^x, where “x” is a real variable and “a” is a real positive constant (a > 0), called the base of the function.  

Recall that for rational exponents, a^m/n= $\sqrt[n]{a^{m}}$

Derivative of the exponential function $a^x$

Let f(x) = a^x, let’s calculate $\frac{d}{dx}a^{x}$

f’(x) = $\frac{d}{dx}a^{x} =~ \lim_{h \to 0} \frac{a^{x+h}-a^{x}}{h} =$[Using the exponential identity a^xa^y=a^x+y, we factor out a^x] $\lim_{h \to 0}a^{x}\frac{a^h-1}{h} = a^{x}·\lim_{h \to 0}\frac{a^h-1}{h}$

Let’s define M(a) = $\lim_{h \to 0}\frac{a^h-1}{h}$. This limit represents the slope of the curve a^x at x = 0 since $\frac{d}{dx}a^{x} \vert_{x=0} =~ a^{0}M(a)=~ M(a)$

In conclusion, the derivative of the exponential function is f'(x) = $\frac{d}{dx}a^{x} = M(a)a^{x}$.

The special role of the number e

Definition. The number e =2.71828182845905…, also known as Euler’s number, is a mathematical constant approximately equal to 2.71828 that can be characterized in several equivalent ways:

1. e = $\lim_{n \to ∞}(1+\frac{1}{n})^n$
2. e = $\sum_{n=0}^\infty \frac{1}{n!}$
3. e is the unique positive number a such that the graph of the function y=a^x has a slope of 1 at x = 0. That is, M(e) = $\lim_{h \to 0}\frac{e^h-1}{h} = 1$ (figure 1.a).

Derivative of $e^x$

Using the general formula $\frac{d}{dx}a^{x} = M(a)a^{x}$, and the fact that M(e) = 1, we obtain $\frac{d}{dx}e^{x} = e^{x}$. The exponential function f(x)=e^x is unique because its derivative equals the function itself.

In particular, f(x) = e^x, $f'(0)$ = $e^{x}|_{x=0} = e^0 = 1$, as expected.

Relating different exponential bases

Let a = 2, f(x) = 2^x. Then, for any constant k, f(kx) = 2^kx = (2^k)^x = b^x where b = 2^k.

$\frac{d}{dx}b^{x} = \frac{d}{dx}f(kx)=$[Differentiate using the chain rule] $kf'(kx)$.

We evaluate at x = 0, $\frac{d}{dx}b^{x}|_{x=0}=kf'(0)$ [Recall the general derivative form for f(x)=2^x, f’(x)=M(2)2^x] =$k·M(2)·2^0 = k·M(2)$. To obtain slope 1 at the origin, we require $k·M(2)=1 \implies[\text{Solve for k: }] k = \frac{1}{M(2)}$. And therefore the corresponding base is $b = 2^k = 2^{\frac{1}{M(2)}}$. This base is by definition the one whose exponential has derivative 1 at 0. That number is what we call e.

Logarithmic functions and their derivatives

The inverse of a^x is the logarithmic function with base a, that is, log_a(x) = y $\iff a^y = x$. The logarithm with base e is called the natural logarithm, denoted ln(x), that is, $\ln(x) = y \iff e^y =x$, (figure 1.b.).

Derivative of ln(x)

Let w = ln(x), we want to calculate $\frac{d}{dx}lnx$.

By definition $w = ln(x) \iff e^w = x$, and differentiating both sides with respect to x, we get: $\frac{d}{dx}e^{w}= \frac{d}{dx} x = 1$

Using the Chain Rule, $\frac{d}{dx}e^{w}=e^{w}\frac{dw}{dx} = $1. Therefore, $\frac{dw}{dx}=\frac{1}{e^w}$ ⇒$\frac{d}{dx}lnx=\frac{1}{x}$

Derivate of $a^x$ using logarithms

Let’s calculate $\frac{d}{dx}a^{x}$. $\frac{d}{dx}a^{x}=~ \frac{d}{dx}((e^{lna})^x)=~ \frac{d}{dx}e^{xlna}$=[The Chain Rule] $e^{xlna}·lna=a^{x}·lna$

Thus, $\frac{d}{dx}a^{x}=(lna)a^{x}$, and therefore M(a) = ln(a).

General logarithmic differentiation rule

For any differentiable function u(x) > 0, $(lnu)'=\frac{d}{dx}ln(u) = \frac{d}{du}ln(u)\frac{du}{dx} =[\text{Previous demonstrated: } \frac{d}{du}(ln(u)) = \frac{1}{u}] \frac{1}{u}u'=\frac{u'}{u}$

Another way of getting the same result regarding $\frac{d}{dx}a^{x}$ is by using the substitution u = a^x, so ln(u) = ln(a^x) = x·ln(a), and therefore, (ln(u))’ = ln(a),

$(lnu)'=\frac{u'}{u}=ln(a) \implies u'=u·ln(a) \implies \frac{d}{dx}a^{x} = (lna)·a^{x}$

Derivative of $log_a(x)$

Let’s calculate $\frac{d}{dx} log_a(x)$. By definition, $w = log_a(x) \iff a^w = x$. Differentiating: $\frac{d}{dx} a^w = \frac{d}{dx} x = 1.$

$\frac{d}{dx} a^w = \frac{d}{dw}a^w\frac{dw}{dx} = a^w·ln(a)\frac{dw}{dx}$ = 1 ⇒ $\frac{dw}{dx} = \frac{1}{a^w·ln(a)}$ ⇒[a^w = x, w = log_a(x)] $\frac{d}{dx}log_a(x) = \frac{1}{x·ln(a)}$

Computing $\lim_{n \to \infin}(1+\frac{1}{n})^{n}$

Take logarithms: $ln((1+\frac{1}{n})^{n})$ = $n·ln(1+\frac{1}{n})$ =[Let $\Delta x=\frac{1}{n}$, then] $\frac{1}{\Delta x}ln(1+\Delta x) =$[Recall ln(1) = 0] $\frac{1}{\Delta x}(ln(1+\Delta x)-ln(1))$

And therefore, $lim_{n \to \infin} ln((1+\frac{1}{n})^{n}) = \lim_{\Delta x \to 0} \frac{1}{\Delta x}(ln(1+\Delta x)-ln(1)) = \lim_{\Delta x \to 0} \frac{ln(1+\Delta x)-ln(1)}{\Delta x}$, and this is $\frac{d}{dx} ln(x)|_ {x=1} =~ \frac{1}{x}|_{x=1} = 1$

$\lim_{n \to \infin}(1+\frac{1}{n})^{n} = lim_{n \to \infin}e^{ln((1+\frac{1}{n})^{n})} =$[Power law for limits] $e^{lim_{n \to \infin} ln((1+\frac{1}{n})^{n})}=$ e¹ = e.

The number e =2.71828182845905…, also known as Euler’s number, is a mathematical constant approximately equal to 2.71828 that can be characterized in many ways. e could be defined as the limit of (1 + ¹⁄_n)ⁿ as n approaches infinity, e = $\lim_{n \to \infin}(1+\frac{1}{n})^{n}.$

Power rule for real exponents

We now justify the power rule for real exponents. Let $r \in \mathbb{R}, x \gt 0$, and u(x)=x^r, then u’(x)=rx^r-1, ∀r ∈ ℝ.

$x^{r}=[\text{Rewrite}]e^{ln(x^{r})}=e^{r·lnx}$ ⇨ $\frac{d}{dx}x^{r}$=[The chain rule]$\frac{r}{x}e^{rlnx}=\frac{r}{x}x^{r}=rx^{r-1}$

Alternatively, using logarithmic differentiation, let $u=x^{r}, ~ln(u)=rln(x) \implies \frac{u'}{u}=\frac{r}{x} \implies u'=\frac{u}{x}r=\frac{x^r}{x}r = rx^{r-1}$

Solved exercises

• $\frac{d}{dx}ln(x)·sin(x) =[\text{Using the product rule}] ln(x)·cos(x)+\frac{sin(x)}{x}$

• $\frac{d}{dx} log_5x^2 =[\frac{d}{dx}log_a(x) = \frac{1}{x\cdot ln(a)} \text{ and Chain Rule}] \frac{2x}{ln(5)·x^2} = \frac{2}{ln(5)·x}$

• $\frac{d}{dx}e^{xtan^{-1}x} =[\text{Using the chain rule and product rule}] e^{xtan^{-1}x}(tan^{-1}x + \frac{x}{1+x^{2}})$

• $\frac{d}{dx} 3e^x+10x^3ln(x) =[\text{Using the sum rule and product rule}] 3·e^x+30·x^2·ln(x)+10x^3\frac{1}{x} = 3·e^x+30·x^2·ln(x)+10x^2.$

• $\frac{d}{dx} (2x^4+1)^{tan(x)}$.

1. y = $(2x^4+1)^{tan(x)}$. Taking the natural logarithm: $\ln(y) = \ln((2x^4+1)^{tan(x)}) = tan(x)ln(2x^4+1)$
2. Differentiate implicitly and considering that tan’(x) = sec²(x): $\frac{1}{y}\frac{dy}{dx} = sec^2(x)·ln(2x^4+1)+ \frac{8x^3}{2x^4+1}·tan(x)$.
3. Solving for $\frac{dy}{dx}$ and substituting y: $\frac{dy}{dx} = y·(sec^2(x)·ln(2x^4+1)+ \frac{8x^3}{2x^4+1}·tan(x)) = (2x^4+1)^{tan(x)}·(sec^2(x)·ln(2x^4+1)+ \frac{8x^3}{2x^4+1}·tan(x)).$

• $\frac{d}{dx}\frac{e^x+e^{-x}}{e^x-e^{-x}}$

$$ \begin{aligned} \frac{d}{dx}\frac{e^x+e^{-x}}{e^x-e^{-x}}= &[\text{Apply the quotient rule: } \frac{d}{dx}\frac{u}{v} = \frac{u'v -uv'}{v^2}] \\[2pt] &= \frac{(e^x-e^{-x})·(e^x-e^{-x})-(e^x+e^{-x})(e^x+e^{-x})}{(e^x-e^{-x})^2} \\[2pt] &= \frac{(e^x-e^{-x})^2-(e^x+e^{-x})^2}{(e^x-e^{-x})^2} \\[2pt] &\text{a²-b² = (a-b)(a+b) where a = eˣ-e⁻ˣ and b = eˣ+e⁻ˣ} \\[2pt] &=\frac{(e^x-e^{-x}-e^x-e^{-x})(e^x-e^{-x}+e^x+e^{-x})}{(e^x-e^{-x})^2} \\[2pt] &=\frac{-2e^{-x}·2e^x}{(e^x-e^{-x})^2} \\[2pt] &=\frac{-4}{(e^x-e^{-x})^2} \end{aligned} $$

• To find the derivative of $\frac{d}{dx} x^x$, we use logarithmic differentiation:

1. Let u = x^x, take the natural logarithm of both sides: ln(u) = x·ln(x).
2. Differentiate implicitly with respect to x: $(ln(u))'=ln(x) + x\frac{1}{x} = ln(x) + 1 \implies \frac{u'}{u}= ln(x) + 1$
3. Solve for $\frac{dy}{dx}=u'$: $u'= u(ln(x)+1) = x^{x}(ln(x)+1).$

Bibliography

1. NPTEL-NOC IITM, Introduction to Galois Theory.
2. Algebra, Second Edition, by Michael Artin.
3. LibreTexts, Calculus. Abstract and Geometric Algebra, Abstract Algebra: Theory and Applications (Judson).
4. Field and Galois Theory, by Patrick Morandi. Springer.
5. Michael Penn, Andrew Misseldine, blackpenredpen, and MathMajor, YouTube’s channels.
6. Contemporary Abstract Algebra, Joseph, A. Gallian.
7. MIT OpenCourseWare, 18.01 Single Variable Calculus, Fall 2007 and 18.02 Multivariable Calculus, Fall 2007, YouTube.
8. Calculus Early Transcendentals: Differential & Multi-Variable Calculus for Social Sciences.