7. Funciones, gráficas y geometría del espacio
7.3. Representación gráfica de funciones.
7.3.1. Funciones elementales: lineales y constantes.
7.3.3. Representación de funciones trigonométricas.
7.3.4. Guardando nuestro trabajo.
7.3.5. Trazando más funciones.
7.3.6. Funciones “a cachitos”.
7.3.7. Crecimiento y extremos relativos.
7.3.8. Asíntotas, concavidad y puntos de inflexión.
7.4. Gnuplot, graficando sin límites.
7.4.1. Instalación y primeros pasos.
7.4.2. Dibujando archivos de datos.
7.4.3. “Como un pro”: creando scripts, afinando nuestros gráficos y exportando los resultados a imágenes.
7.5. Mira mamá: “funciones en 3D”.
7.1. Nuestra primera gráfica.
¿Qué es una
gráfica? Es una forma de representación de los datos de una forma
visual, atractiva  que nos permite
interpretarlos y retenerlos más eficientemente.
que nos permite
interpretarlos y retenerlos más eficientemente.
Para realizar nuestra primera gráfica utilizaremos OpenOffice.org Calc, la hoja de cálculo del paquete ofimático libre OpenOffice. Es una suite gratuita y multiplataforma que incluye un procesador de textos (Writer), una hoja de cálculo (Calc), un gestor de presentaciones (Impress), un editor de gráficos (Draw) y un gestor de bases de datos (Base). Puedes descargarlo para Windows desde es.openoffice.org, si utilizas GNU/Linux seguramente lo tendrás ya instalado.
|
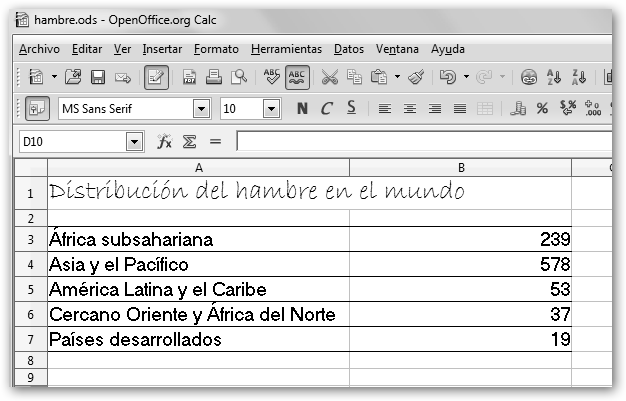
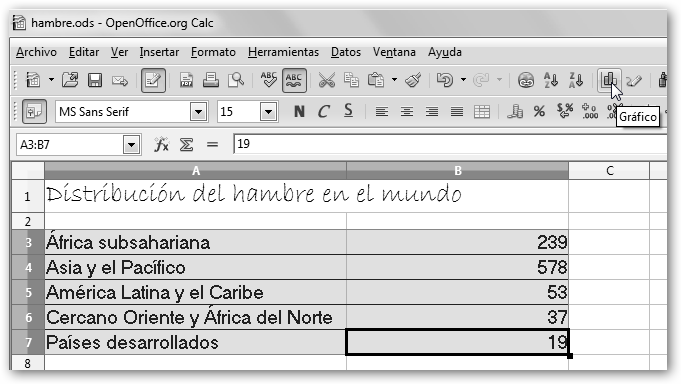
Lo primero que realizaremos una vez abierto OpenOffice.org Calc (Inicio, Todos los programas, OpenOffice.org 3.1, OpenOffice Calc) es crear una tabla para introducir los datos. En el ejemplo se ilustra la distribución del hambre en el mundo por zonas tal como se recoge en el informe de la FAO. |
|
|
Estos datos se encuentran disponibles en la Web de la FAO sobre el hambre en el mundo: www.fao.org/hunger/hunger-home/es/. Seleccionamos toda la tabla con un clic sostenido (observa desde la celda A3 hasta la celda B7) y hacemos clic en el botón Gráfico de la barra de herramientas o en la opción Gráfico del menú Insertar. |
|
|
Los documentos en Calc se organizan en libros, cada uno de los cuales tiene un número de hojas. Cada hoja es una colección de celdas y éstas se organizan de forma matricial por filas (se identifican por números 1, 2, 3, …) y columnas (utilizamos letras: A, B, C, …). |
|
|
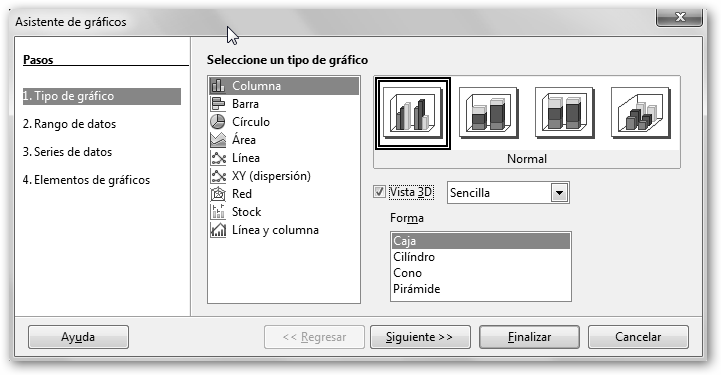
Nos aparecerá un asistente para la creación de la gráfica. En el primer paso debemos seleccionar el tipo de gráfico: Columna, Barra, Círculo (gráfico de tartas), Área, etc. Además para mejorar la apariencia de la presentación elegiremos la Vista 3D. |
|
|
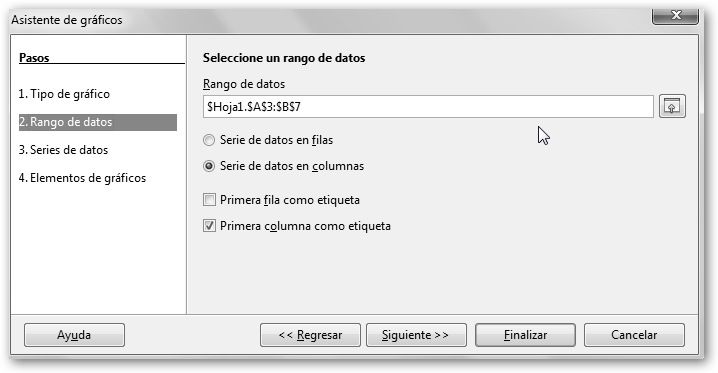
Observa que los gráficos de columna en Calc pueden ser en 3D y tener la forma tradicional de Caja, pero también otras menos convencionales: Cilindro, Cono y Pirámide. Pulsamos Siguiente para continuar en el siguiente paso del asistente. Continuamos confirmando que el rango de datos para la gráfica es correcto. En el ejemplo $Hoja1.$A$3:$B$7. |
|
|
Además, indicamos que los datos están distribuidos por columnas (Serie de datos en columnas) y que de las dos columnas, la primera (A) contiene las etiquetas (en este caso las zonas geográficas), Primera columna como etiqueta. Nuestra tabla de datos muestra el número de personas que padecen hambre en las diferentes zonas geográficas del mundo. Las zonas (etiquetas) se presentan en la primera columna (A) y el número asociado (los datos) en la segunda (B). |
|
|
Expliquemos detenidamente que significa el texto que aparece en el cuadro Rango de datos: * $Hoja1. Como hemos comentado en Calc los documentos se denominan libros. Un libro consta de varias hojas, en nuestro caso estamos trabajando con la primera hoja ($Hoja1). * $A$3:$B$7. El rango de datos que queremos graficar se extiende desde la celda situada en la columna A y fila 3 (África subsahariana) hasta la celda que se encuentra en la columna B y la fila 7 (19, hambre en los países desarrollados) |
|
|
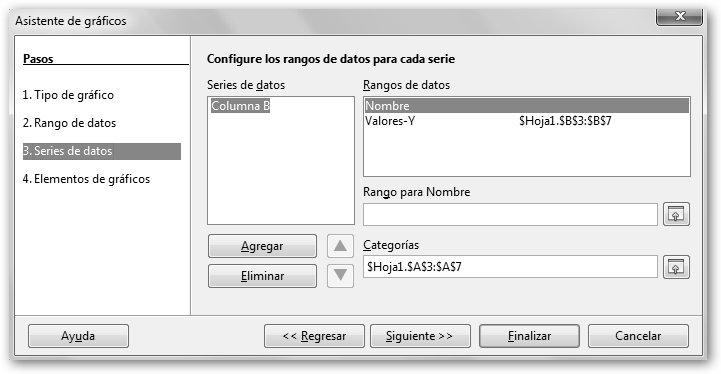
En el paso 3 se nos muestra que las etiquetas se encuentran en $Hoja1.$A$3:$A$7, es decir, en las celdas de las filas 3 a la 7 de la columna A y los Valores-Y en las celdas de las filas 3 a la 7 de la columna B ($Hoja1.$B$3:$B$7). |
|
|
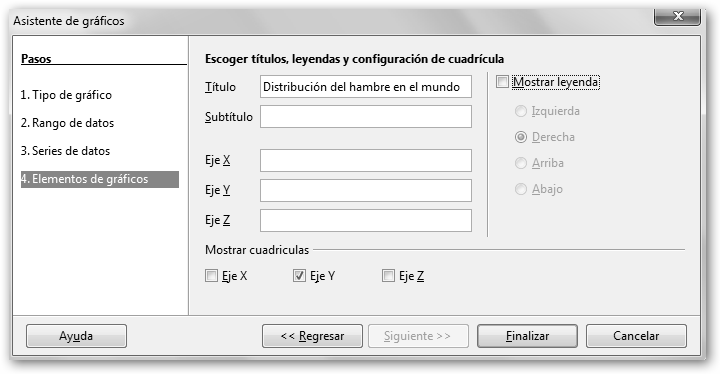
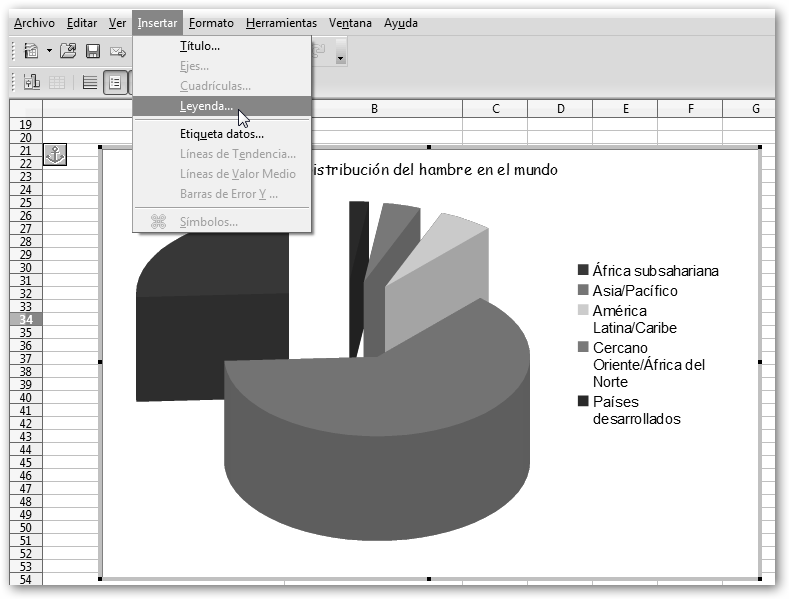
En el último paso del asistente configuramos los diferentes elementos de la gráfica: título (Distribución del hambre en el mundo), subtítulo, si queremos mostrar o no cuadrículas en los ejes X, Y, Z y la leyenda (si la vamos a tener indicaremos donde ubicarla). Hacemos clic en Finalizar para acabar el asistente. |
|
|
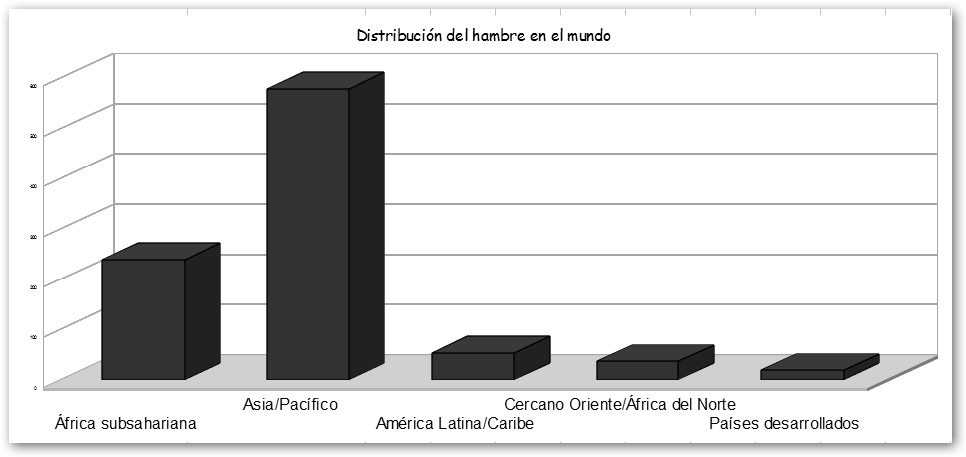
Observa el gráfico que hemos obtenido con el asistente. La interpretación es clara, en África subsahariana, Asia y el Pacífico es donde el problema del hambre es más grave. |
|
|
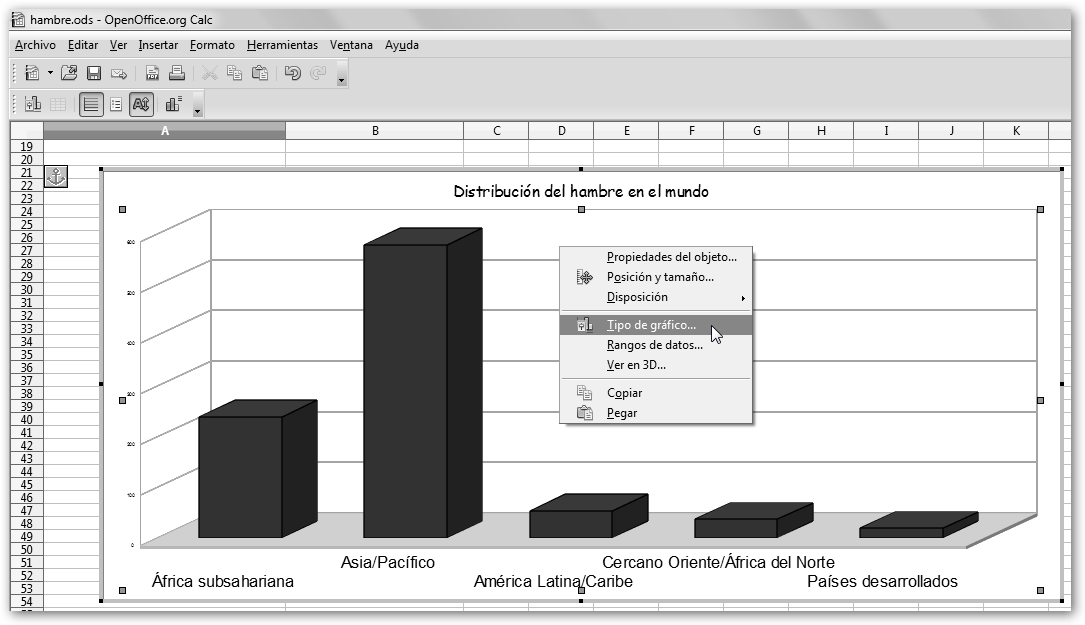
Haciendo doble clic sobre el gráfico procederemos a editarlo. Podremos modificar: * el Tipo de gráfico…: sustituirlo por un gráfico de barras, de tartas, Área, etc. * el Rango de datos… * Cambiar el estilo y el tamaño del título o de las etiquetas, etc. |
|
|
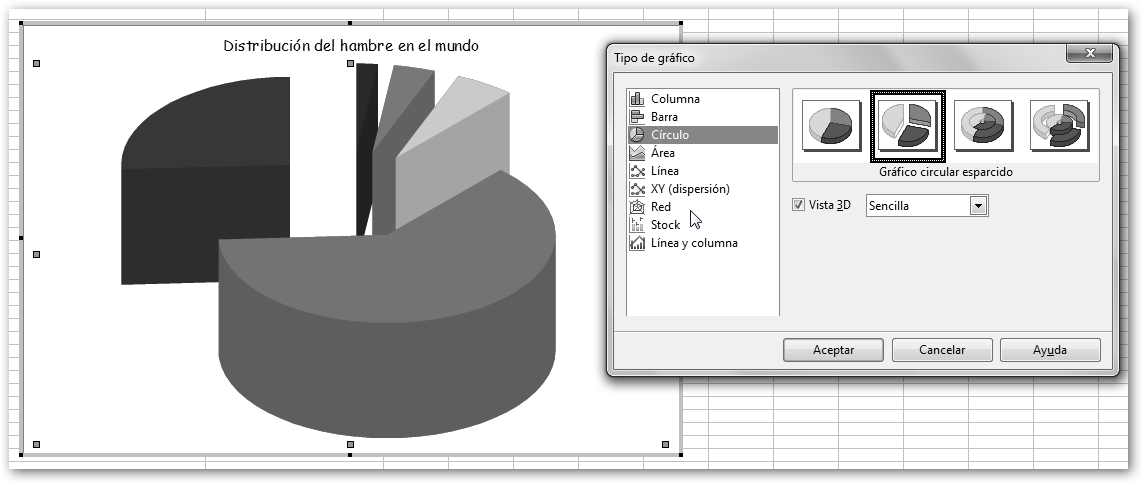
Por ejemplo, haz clic con el ratón derecho en el gráfico y selecciona la opción del menú contextual Tipo de gráfico y cámbialo por el gráfico circular esparcido con Vista 3D, Sencilla.
|
|
|
Para añadir la leyenda elige la opción Leyenda… del menú Insertar tal como se ilustra en la figura e indica donde se mostrará. Una vez creada la leyenda, haz clic sobre ella con el botón derecho del ratón y selecciona Propiedades del objeto… para cambiar la fuente, el estilo, color y tamaño del texto, los bordes, etc. |
|
7.2. Función ¿de qué?
Una función es una
relación que hace corresponder a cada elemento de un conjunto X uno y solo
un elemento de otro conjunto Y (formalmente sería:
![]() es una función de X a Y sii
es una función de X a Y sii
![]()
![]()
 ).
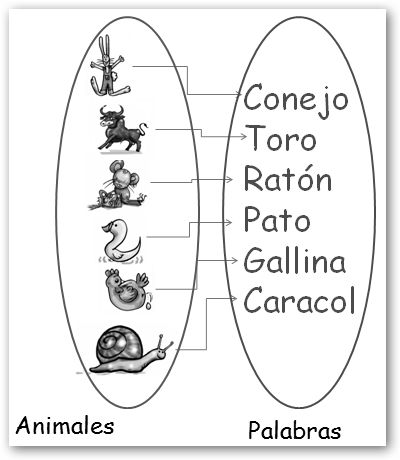
Podemos crear una función entre cualquier tipo de conjuntos,
por ejemplo, un conjunto de animales y otro de palabras, la
llamaremos la función diccionario:
).
Podemos crear una función entre cualquier tipo de conjuntos,
por ejemplo, un conjunto de animales y otro de palabras, la
llamaremos la función diccionario:
Sin
embargo, la mayoría de las funciones serán funciones
reales como la siguiente,![]() ,
f(x)=x2+4x+5, f(x)=sin2(x), f(x)=ex,
etc.
,
f(x)=x2+4x+5, f(x)=sin2(x), f(x)=ex,
etc.
7.3. Representación gráfica de funciones.
Vamos a representar funciones
con distintas herramientas para que te familiarices con todas ellas y elijas las que
más se adapten a tus necesidades y requerimientos: sistema operativo en el que
trabajas, el ancho de banda de tu conexión a Internet (en algunos centros
educativos la conexión va a pedales
 ), el tipo de gráficos, facilidad de uso, etc.
Utilizaremos los siguientes programas:
), el tipo de gráficos, facilidad de uso, etc.
Utilizaremos los siguientes programas:
* KmPlot: es el trazador de funciones del entorno KDE, uno de los gestores de ventanas más importantes del sistema operativo GNU/Linux y forma parte de su proyecto educativo KDE Education Project. En Ubuntu se instala desde Aplicaciones, Centro de software de Ubuntu y busca e instala kmplot. Su página Web es edu.kde.org/kmplot y su manual en línea está en docs.kde.org/stable/es/kdeedu/kmplot. En la actualidad, no existe desafortunadamente una versión para Windows aunque puedes utilizar la iniciativa KDE Windows Initiative, windows.kde.org para conseguir portar esta aplicación KDE a Windows.
* Octave la alternativa libre a Matlab (www.gnu.org/software/octave/) disponible para Windows (octave.sourceforge.net) y GNU/Linux, así como, su front-end QtOctave (solo para GNU/Linux), es decir, una aplicación que trata de hacer el manejo de Octave más amigable pero que no es más que una interfaz gráfica a dicho programa. En Ubuntu navega por Aplicaciones, Centro de software de Ubuntu y busca e instala GNUOctave y QtOctave, en la consola los paquetes que te interesan son: octave y qtoctave.
7.3.1. Funciones elementales: lineales y constantes.
|
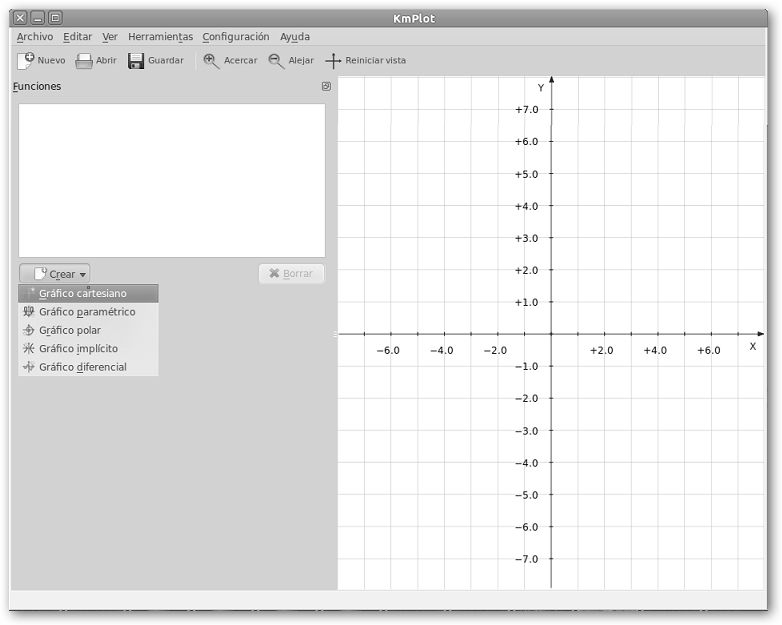
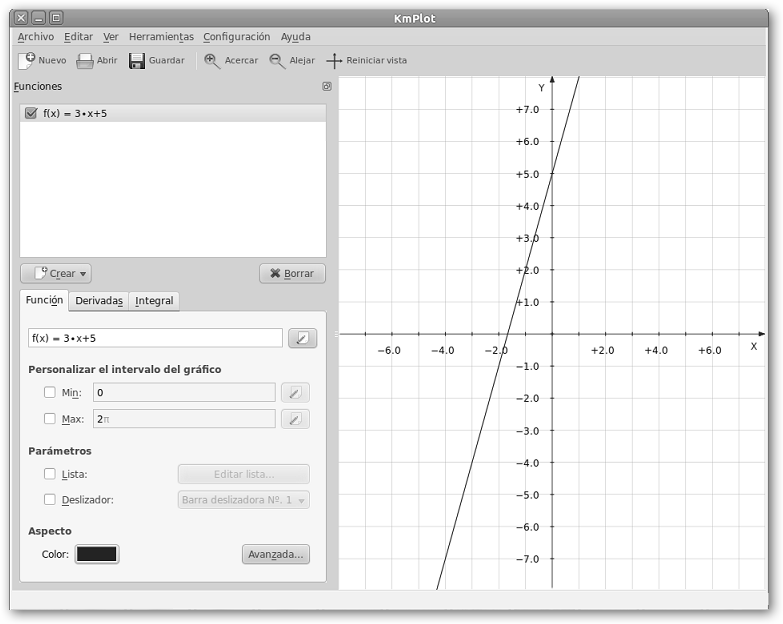
Una vez lanzado desde Aplicaciones, Educacion, KmPlot haz clic en Crear, Grafico cartesiano. A continuación, escribe la función, en el ejemplo f(x)=3*x+5 y pulsa INTRO. Hemos creado una función lineal: y = m*x +b y se representa por una recta con pendiente m. b es la ordenada en el origen, es decir, el valor que toma “y” cuando “x” es cero o el punto de corte de la recta con el eje de ordenadas (el vertical Y). |
|
|
Fíjate que podemos personalizar el intervalo de la gráfica, cambiar el aspecto modificando el color, el ancho y el estilo (sólido, punto, traza, raya, raya punto) de línea (sección Aspecto, pulsa en el botón Avanzada…), asignarle un nombre, etc. A continuación, hemos graficado tres funciones más.
|
|
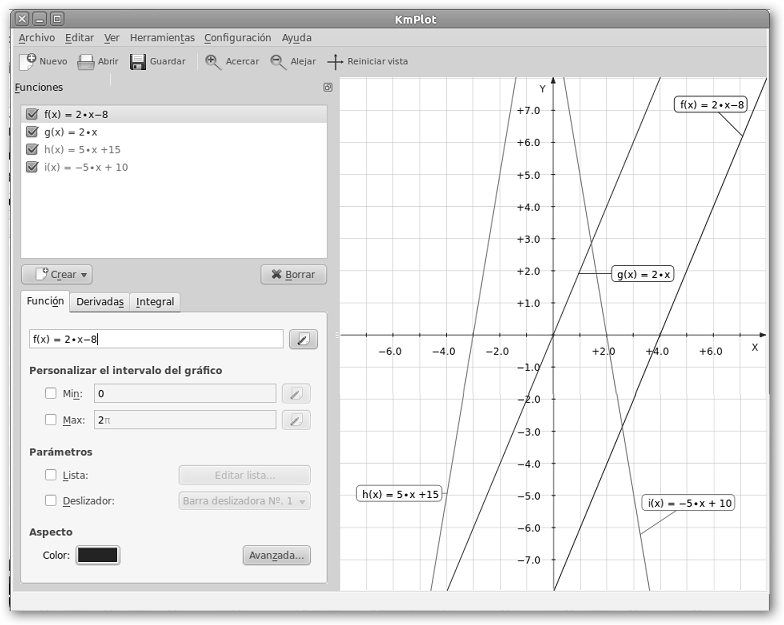
Comprueba que la función 2*x pasa por el origen pues su ordenada en el origen es 0. Además, observa que las rectas 2*x y 2*x-8 son paralelas, la única diferencia entre ellas es que la primera pasa por el origen de coordenadas y la segunda está desplazada hacia la derecha. Cuando las pendientes no son iguales, las rectas son secantes y se cortarán en algún punto.
El punto de corte con el eje Y de la recta y=m*x+b, es 0=m*x+b, x=-b/m, es decir, (-b/m, 0) que en el ejemplo de la recta 2*x-8 es (4, 0). Compruébalo: –(-8) /2 = 8/2=4. Se debe señalar que las funciones lineales no tienen ni máximos ni mínimos.
|
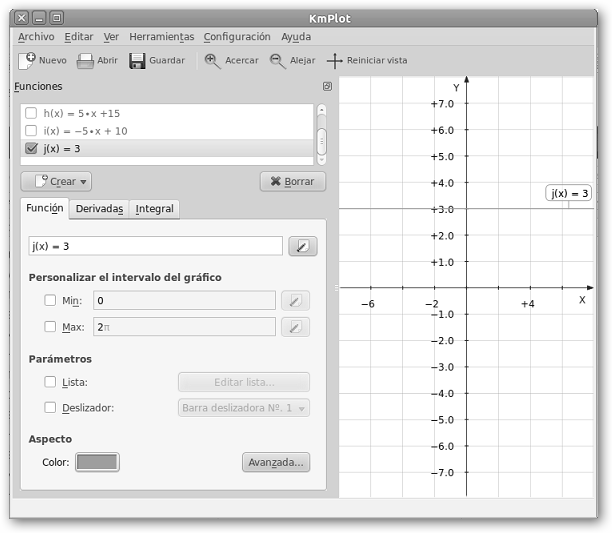
También es interesante que te des cuenta que 5*x+15 es creciente pues su pendiente (5) es positiva, todo lo contrario sucede a -5*x+10 que es decreciente al tener una pendiente (-5) negativa. Un caso particular de las funciones lineales son las funciones constantes donde la pendiente vale cero (m=0). En este caso, la forma general sería y=b y son rectas paralelas al eje X (en la figura se ilustra y=3). |
|
7.3.2. Parábolas a tutiplén.
|
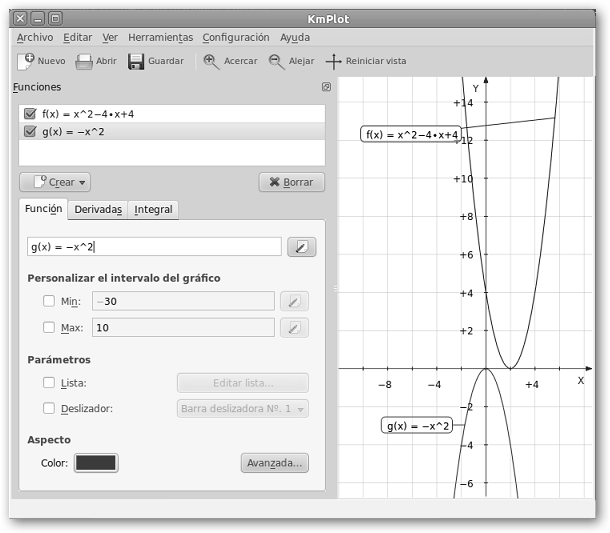
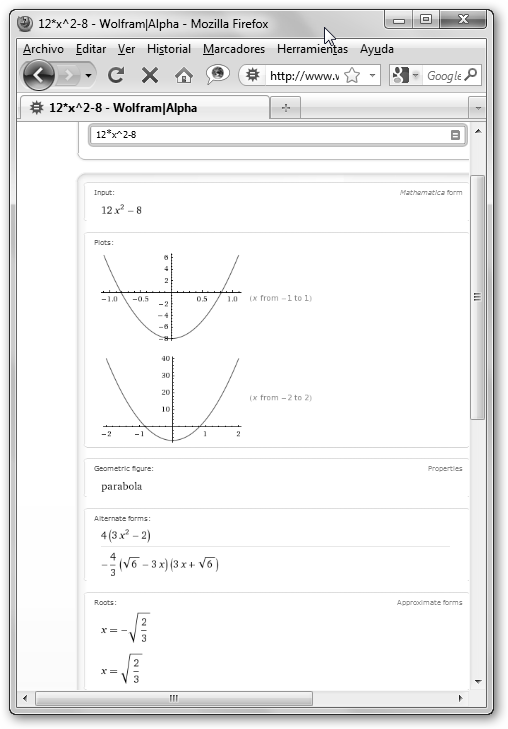
La representación de las funciones cuadráticas, aquellas de la forma ax2+bx+c es una parábola. Observa que ambas cortan al eje x en solo un punto porque solo tienen una raíz. Recuerda que el discriminante es Δ=b2-4ac y sería (-42)-(-4)*1*4=16-16=0 y 02-4*(-1)*0=0 para x2-4x+4 y -x2 respectivamente. Recuerda: * Δ=0, 1 sola raíz real. * Δ>0, 2 raíces reales. * Δ<0, 2 raíces imaginarias. |
Además, la primera parábola (x2-4x+4) abre hacia arriba porque el primer término (a=1) es positivo. La segunda (-x2) abre hacia abajo porque el primer término es negativo (a=-1). |
|
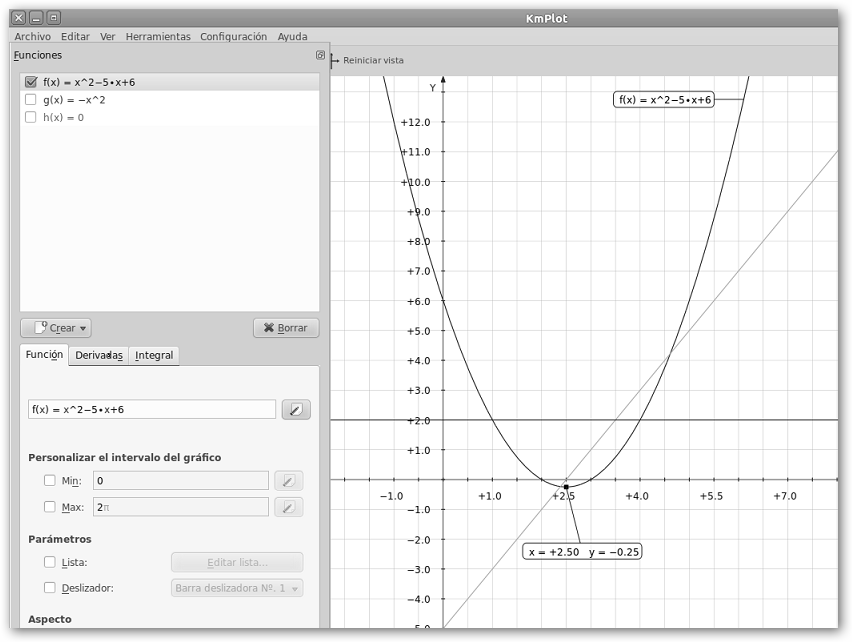
La representación de x2-5*x +6 muestra una parábola que corta al eje X en dos puntos (x=2 y x=3) puesto que el discriminante es positivo (Δ=b2 -4ac = (-5)2-4*1*6=1>0) lo que implica que tiene dos raíces reales. Observa que abre hacia arriba (a=1>0) y el mínimo se encuentra en (2.50, -0.25). Para solicitar a KmPlot que lo muestre navega por Herramientas, Encontrar mínimo… y en Aspecto, Avanzada… seleccionar Mostrar extremos (puntos mínimo y máximo). |
|
|
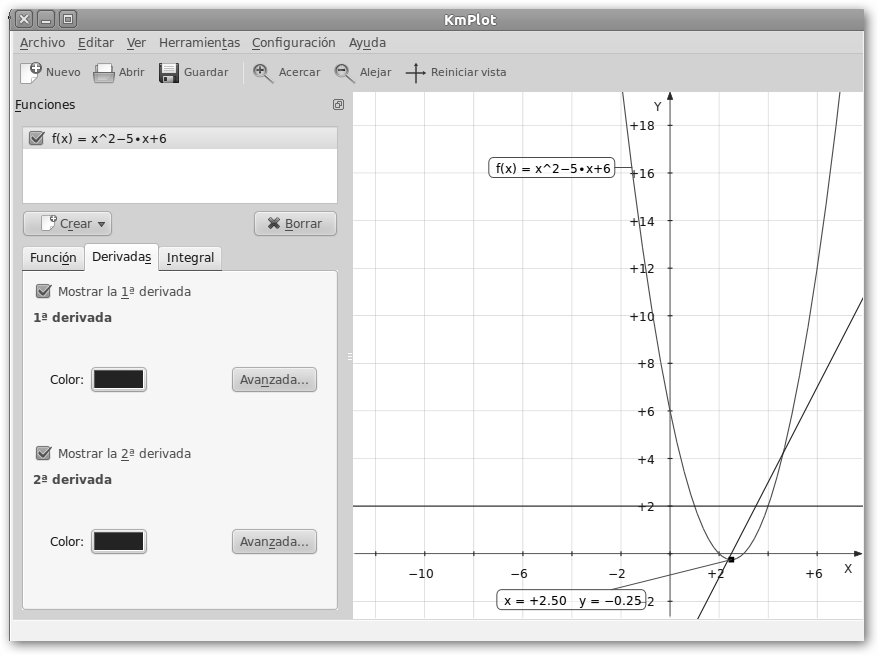
Además, se pueden obtener las derivadas primera (2x-5) y segunda (2). Navega a la pestaña Derivadas en el panel inferior izquierdo para que KmPlot las trace. También, puedes pedir que represente la Integral. La derivada 2x – 5 tiene una raíz en x=-b/m=5/2=2.5. |
|
|
En el intervalo (-∞, 2.5), la derivada f’(x)=2x-5 es negativa y, por tanto, nuestra función f(x) es decreciente. En (2.5, +∞), la derivada es positiva y nuestra función es creciente. |
|
|
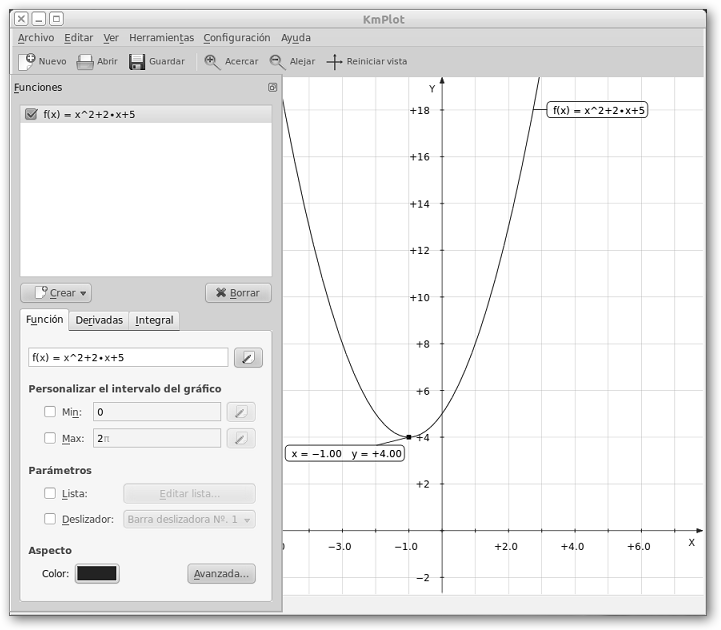
La última parábola que enseñaremos será x2+2x+5. No corta al eje X porque como su discriminante es negativo (Δ = b2-4ac = -16) tiene dos raíces imaginarias: -1 -2i, -1+2i. Abre hacia arriba (a=1>0) y hemos solicitado nuevamente que nos muestre el mínimo de la función. |
|
7.3.3. Representación de funciones trigonométricas.
|
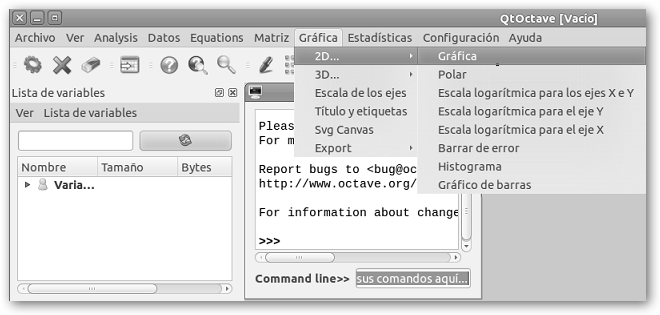
En GNU/Linux realiza lo siguiente: 1. Abre QtOctave desde Aplicaciones, Ciencia, QtOctave. 2. Navega por Gráfica, 2D…, Gráfica. |
|
|
3. En la ventana que te aparece en el cuadro de texto x escribe -10:0.1:10, es decir, queremos representar la función desde x=-10 hasta x=10, 0.1 indica la precisión, el número de puntos que queremos que se grafiquen. Se tomarán valores desde -10 hasta 10 incrementando una variable 0.1. Si lo incrementas sólo 0.01 tendrás mayor resolución. |
|
|
|
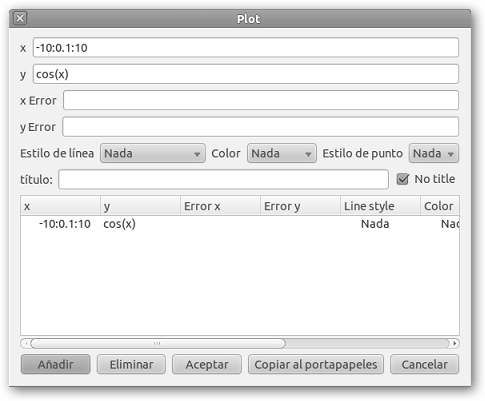
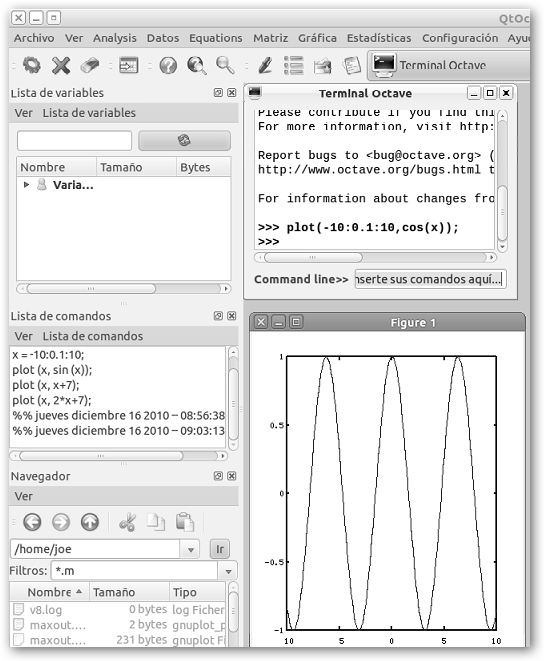
4. A continuación, tecleamos en “y” la función: cos(x). Luego hacemos clic en Añadir y posteriormente en Aceptar. Observa que gráficamente podíamos cambiar el Estilo de línea (líneas, puntos, cuadros, pasos, etc.), el Color y el Estilo de punto (+, *, 0, x). 5. En el Terminal Octave puedes observar la orden que se ejecuta: plot(-10:0.1:10, cos(x)) y en la esquina inferior derecha la gráfica. El Terminal Octave es la consola donde se pueden ejecutar todas las órdenes de Octave. |
|
|
|
|
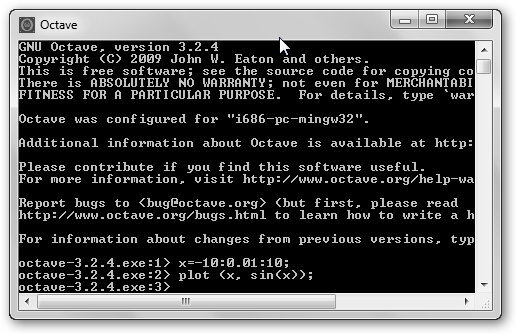
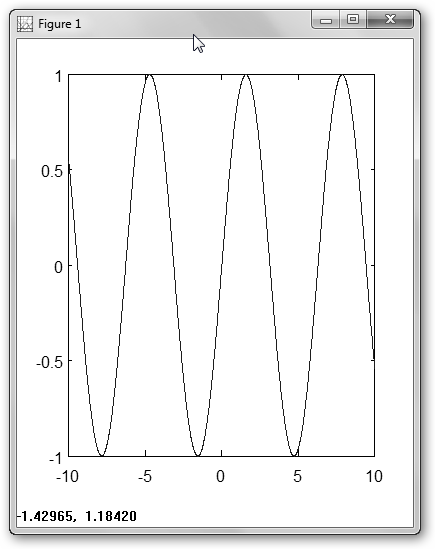
En Windows navega por Inicio, Todos los programas, GNU Octave 3.2.4, Octave y escribe las órdenes que se muestran en la figura. Hay dos diferencias: la primera es que indicamos el rango en una instrucción previa a plot, la segunda es que dibujaremos la función seno (plot(x, sin(x)). |
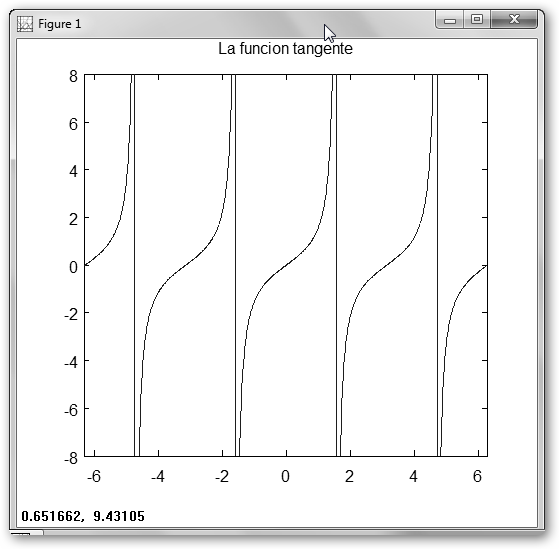
Representemos ahora la función tangente. |
|
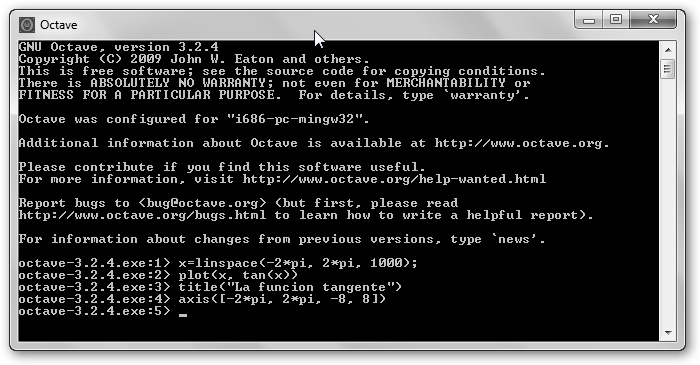
1. Obtenemos primero un vector con linspace(mínimo, máximo, N); en este caso, queremos 1000 puntos en el intervalo [-2Π,2 Π]. 2. Dibujamos la función tangente con plot(x, tan(x)) pero no cerramos con punto y coma para seguir “retocando” la gráfica. 3. Le damos un título: title(“La función tangente”). 4. Con axis([-2*pi, 2*pi, -8, 8]) definimos la escala, los límites del eje x ([-2Π,2 Π]) y del eje y ([-8, 8]). En Windows también podemos graficar con WGnuplot y Microsoft Mathematics entre otros. |
Por supuesto tenemos muchas más opciones, por ejemplo: * plot(x, tan(x), ‘b’) dibujaría la tangente en azul (blue, azul) y/o podemos cambiar los tipos de líneas y símbolos, sustituye la b por: ‘r’ roja, ‘y’ amarilla, ‘.’ grafica con puntitos, ‘o’ puntitos más gordos; +, *, s, d, dibuja con +, *, □ y ◊. * Para escribir leyendas en los ejes: Xlabel(“Eje x”), ylabel(“Eje y”). |
7.3.4. Guardando nuestro trabajo
Algo que siempre es interesante realizar es guardar nuestro trabajo para así poder recuperarlo en cualquier momento.
|
|
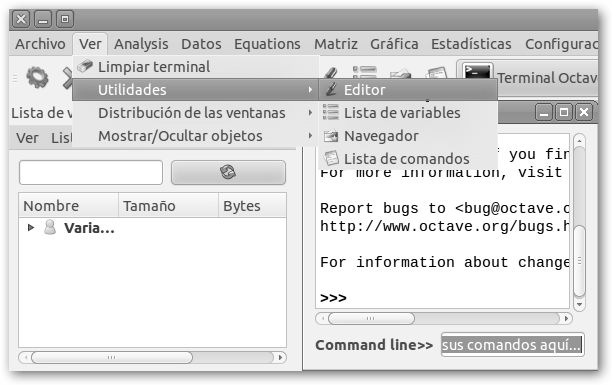
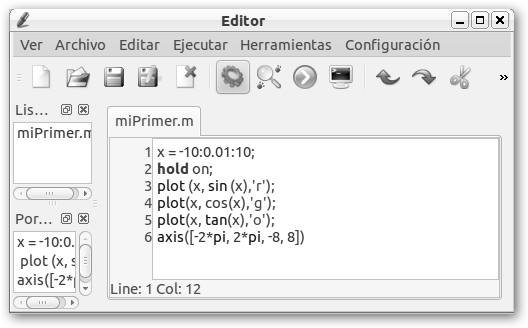
Vamos a explicarlo con QtOctave, sigue los siguientes pasos: 1. Lánzalo desde Aplicaciones, Ciencia, QtOctave. 2. Navega por Ver, Utilidades, Editor para crear un fichero con extensión .m donde guardaremos nuestro trabajo. 3. Selecciona la opción Guardar del menú Archivo y asígnale un nombre al fichero, en el ejemplo, lo llamaremos miPrimer.m. 4. Escribe las órdenes o instrucciones Octave. 5. Guarda nuevamente el trabajo haciendo clic en el disco flexible o disquete, desde el menú Archivo, Guardar o con las teclas rápidas Ctrl + S (S es de Save, guardar en inglés). 6. Ejecuta el programa con
la herramienta ejecutar 7. En cualquier momento
podrás recuperar tu trabajo desde la herramienta Abrir
|
|
|
|
|
|
|
|
|
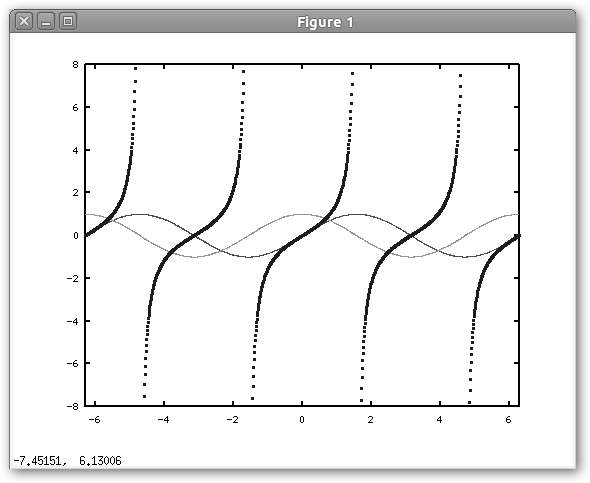
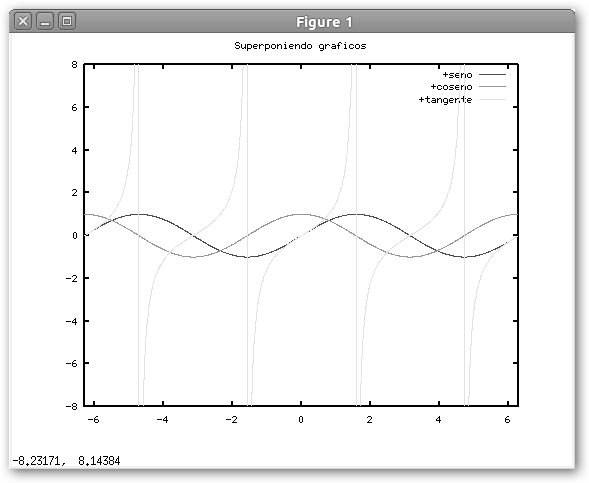
Observa el resultado obtenido. Hemos solicitado a Octave realizar el trazado de tres funciones: seno en color rojo, coseno en verde y tangente en naranja. Debe llamarte la atención la instrucción hold on, con ella lo que realizamos es indicar a Octave que vamos a superponer varios gráficos.
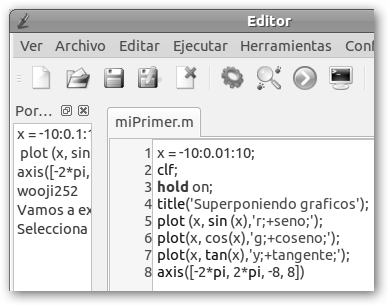
En este ejemplo hemos utilizado la instrucción clf para borrar o limpiar la ventana gráfica y añadido una leyenda a las funciones: plot(x, sin(x), ‘r;+seno;’); y al gráfico (title(“Superponiendo gráficos”)). |
|
|
7.3.5. Trazando más funciones.
Veamos ahora otras funciones, a saber:
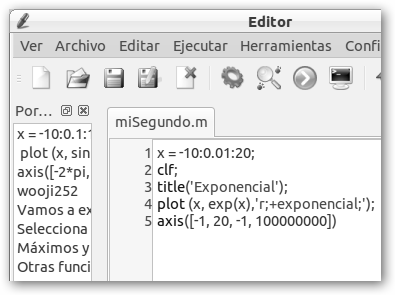
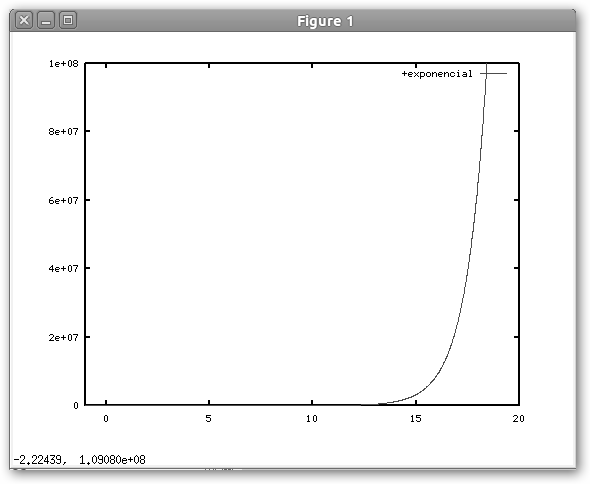
* Exponencial: se trata de la función f(x)=ex donde “e” es el número de Euler. Es continua y creciente y se verifica que ex+y = ex ey, ex-y= ex /ey, e0 =1, e-x =1/ex, (ex)’= ex. Se trata de un caso particular de la función exponencial con base “a” donde “a” es un número real positivo f(x)= ax y observa el crecimiento absolutamente desproporcionado que obtenemos cuando no hemos alcanzado aún el valor x=20.
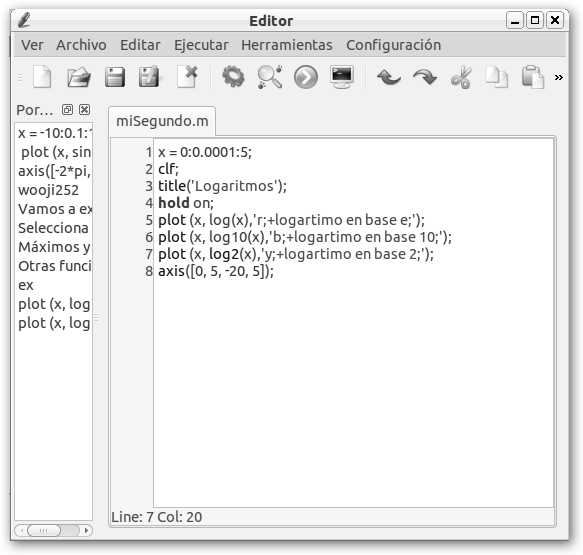
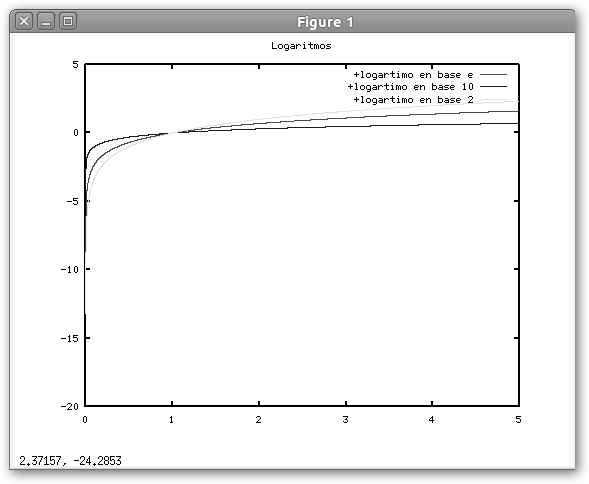
* Funciones logarítmicas: función inversa a la exponencial, el logaritmo en base “a” se representa como y=logax. Un número n= logax si y solo si an=x, por esta razón loga1=0 independiente de la base “a”, pues a0 es siempre 1. Un caso particular es el logaritmo neperiano o logaritmo natural (ln) que es la función logaritmo con base “e”. Se trata de una función creciente y cuyo dominio son los números positivos, es decir, x siempre debe ser cero.
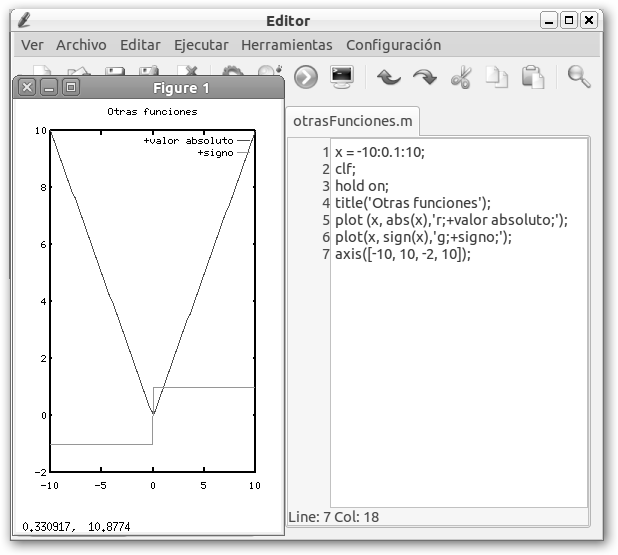
* Función signo: aquella que devuelve el signo del número, es decir, si es positivo devuelve 1, si es cero, 0 y si es negativo -1.
* Valor absoluto: devuelve el
valor numérico de un número independientemente de su signo, es decir:
![]()
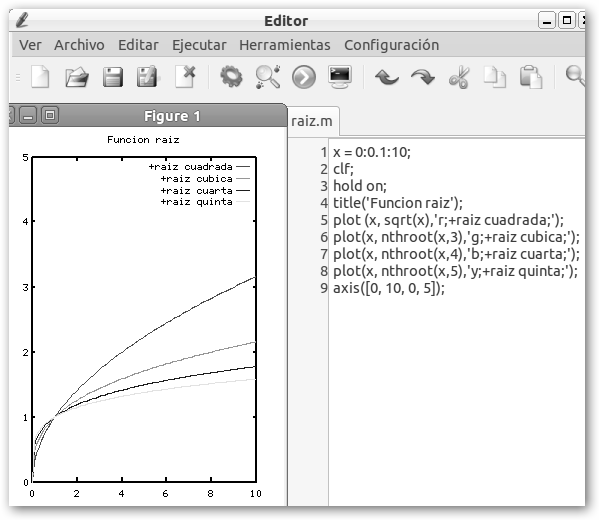
* Función raíz: es
la función inversa de la potencia, es decir, y es la raíz
n-ésima de x (y= ![]() ) si se cumple que
yn=x, por ejemplo, 2=
) si se cumple que
yn=x, por ejemplo, 2=![]() pues 23=8.
pues 23=8.
|
Detalles del programa que grafica la exponencial y el resultado de su ejecución. |
Si tienes dudas escribe en el terminal Octave: help orden o doc orden, por ejemplo: help plot, help exp, etc. |
|
Observa la representación del logaritmo neperiano o natural y de los logaritmos en base 10 y 2. Observa como todas las gráficas en x=1 valen cero. |
Mostramos para finalizar el trazado de la función módulo o el valor absoluto, la función signo y la raíz cuadrada, cúbica, cuarta y quinta. |
|
|
|
7.3.6.Funciones “a cachitos”.
No, tranquilo, no es que las
funciones se caigan a pedazos.  . Realmente se llaman
funciones por partes y son aquellas cuya definición varía dependiendo de la
variable x, por ejemplo:
. Realmente se llaman
funciones por partes y son aquellas cuya definición varía dependiendo de la
variable x, por ejemplo:
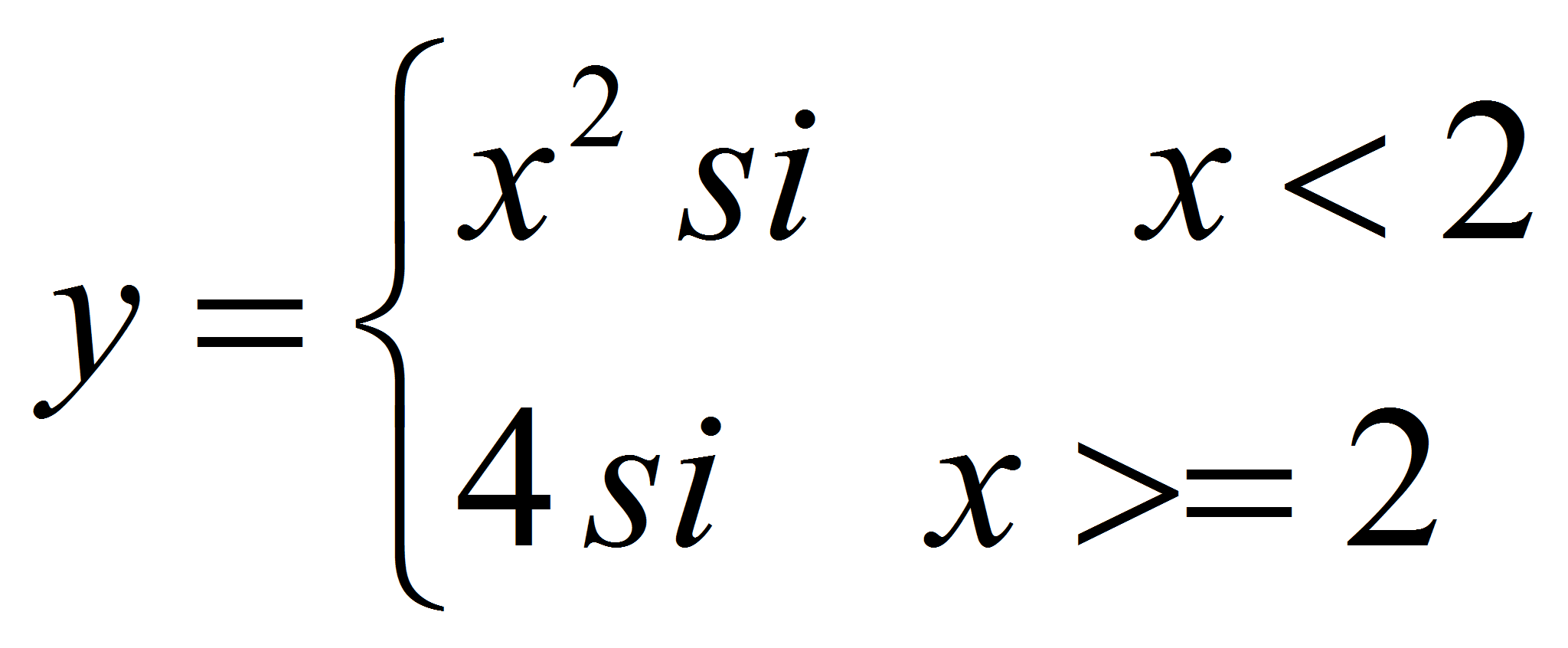
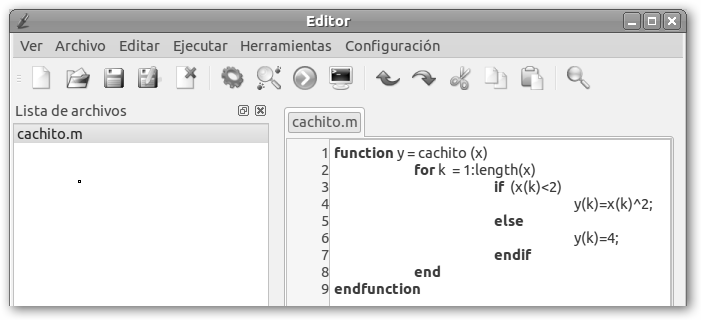
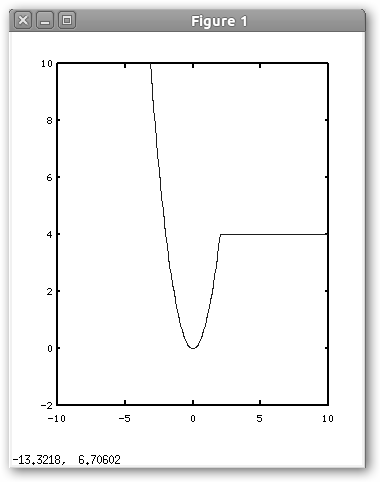
Para dibujarlas crearemos una función en Octave. ¡Cuidado con la sintaxis!, la función cachito tiene como argumento un vector (x) y devuelve otro vector (y).
|
Internamente la función itera por el vector x (for k=1:length(x)) y almacena en y(k), x(k)2 o 4 en función de si x(k) es menor o no que 2. “Si estás más pegado que un sello”, ten en cuenta que length(x) devuelve la longitud del vector x (length({1, 4, 9}) devuelve 3), y(k) es el elemento k-ésimo del vector y (y={1, 4, 9, 16, 25}, y(3) es 9, y(4) es 16…). |
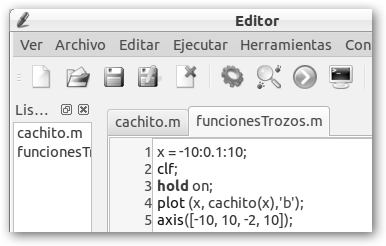
Es importante que observes que hemos guardado la función en un fichero llamado cachito.m, es decir, el mismo nombre que la función.
|
|
Finalmente, dibujamos nuestra función. Observa que es continua, es decir, si quisiéramos dibujarla no tendríamos que separar el lápiz del papel. Sustituye en nuestra función cachito el 4 por el 7, la llamada plot (x, cachito(x), 'bo'); y verás que es discontinua. |
7.3.7. Crecimiento y extremos relativos.
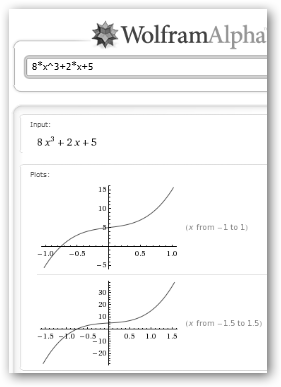
Para conocer las propiedades de las funciones nada mejor que WolframAlpha en www.wolframalpha.com.
|
Una función f es creciente en un intervalo I si siempre que tengamos dos puntos (a, b) donde a sea menor que b (a<b) en I entonces f(a) < f(b). Si siempre sucediera que f(a) > f(b) entonces sería decreciente. En el último caso, si siempre ocurre que f(a)=f(b) entonces es constante en dicho intervalo.
Gráficamente cuando se eleva la gráfica de la
función entonces es creciente, si va “cuesta abajo y
sin frenos
Para conocer los
intervalos de crecimiento emplearemos la derivada de la función
y, más concretamente, sus raíces. Definiremos los
intervalos I entre las raíces. En aquellos donde el signo es positivo
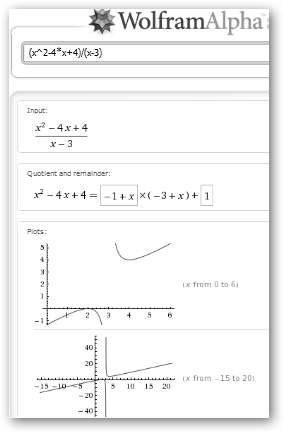
(f’(x)>0 Veamos otro ejemplo más complejo. Véase la función y la gráfica de la figura realizada con Wolfram. Recordemos primero la fórmula de la derivada de un cociente de funciones:
|
Por ejemplo, la función de la figura f(x)=8x3+2x+5, tiene como derivada f’(x)=24x2+2 que es mayor que cero para todo x, luego es siempre creciente.
|
|
En el ejemplo que estamos trabajando, la derivada f’(x) sería la siguiente fórmula matemática: |
|
|
Estudiamos el
signo en los tres intervalos que podemos formar con sus dos raíces
(2, 4): (- 1. x<2: (x-2) < 0, (x-4) < 0, f’(x) > 0, f es creciente. 2. 2<x<4:(x-2) >0, (x-4) < 0, f’(x) < 0, f es decreciente. 3. x>4: (x-2) >0, (x-4) > 0, f’(x) > 0, f es creciente. De lo anterior se deduce gráficamente que 2 es un máximo relativo y 4 un mínimo relativo. Matemáticamente calculamos la derivada 2ª |
|
|
f’’(x)= Si para las raíces “r” de la derivada de nuestra función (2, 4), obtenemos f’’(r) <0 entonces tenemos un máximo relativo; si es f’’(r) >0 será un mínimo relativo. f’’(2)=2/(-1)=-2<0, 2 es un máximo relativo y f’’(4)=2/1=2>0, 4 es un mínimo relativo. |
Detalle de la misma pantalla anterior. |
7.3.8. Asíntotas, concavidad y puntos de inflexión.
|
Una asíntota es una recta a la que nuestra función
se va acercando o aproximando indefinidamente, es como el cobrador
del frac del moroso Existen tres
tipos de asíntotas: horizontales, verticales y oblicuas. La
tangente tiene infinitas asíntotas verticales,
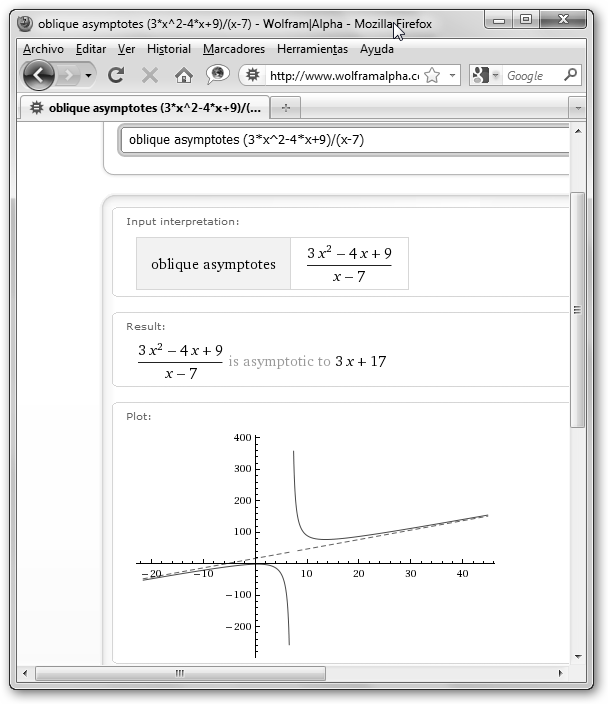
Se solicitan a WolframAlpha con las órdenes asymptotes función y oblique asymptotes función. |
Las asíntotas de tan(x) son Πn+Π/2, siendo “n” un número entero, es decir: Π/2, 3Π/2, 5Π/2, 7Π/2,… -Π/2, -3Π/2, -5Π/2,… |
|
Observa
que como te indica WolframAlpha
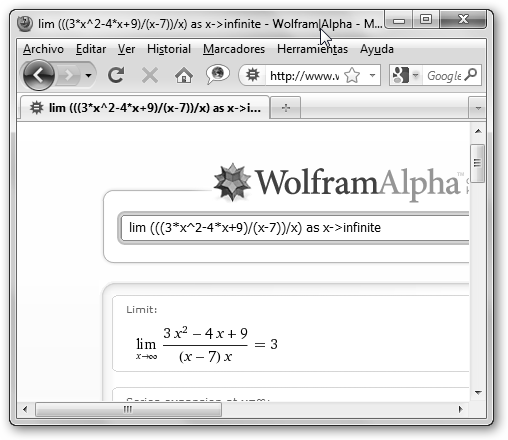
Además,
puesto que
|
|
|
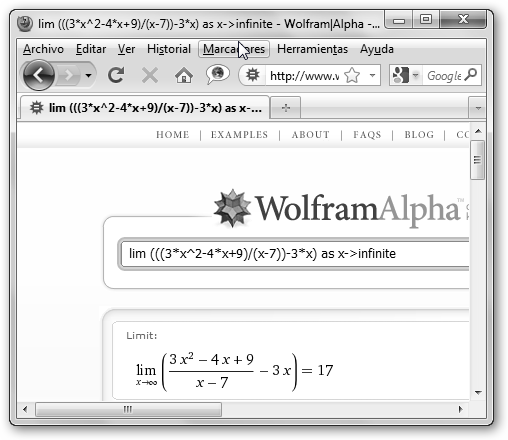
Y para obtener b, debemos calcular el límite al infinito de la función –m x:
|
Otro ejemplo más sencillo es 2*x+1/x, su asíntota oblicua es 2x. Al dividir la función por x el límite es 2 y al restarlo a 2x es 0. |
|
Detalles donde solicitamos a Wolfram los límites que precisamos. |
|
|
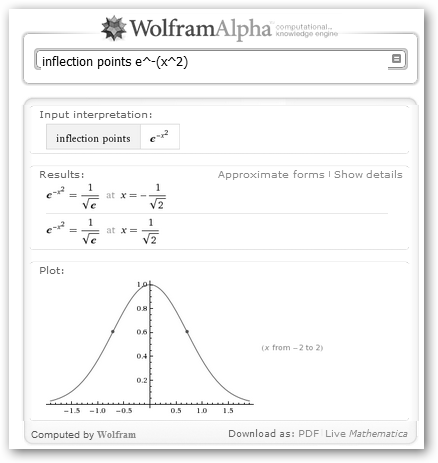
Para preguntar a WolframAlpha los puntos de inflexión de una función basta con escribir inflection points función. Una función
es cóncava hacia arriba o convexa en un intervalo si
para todo punto de dicho intervalo, la derivada segunda, si
existe, es positiva (f’’(x)>0
Calculemos la
derivada segunda de x4-4x2. La derivada primera es
4x3-8x y la segunda es 12x2-8. Luego x=
|
|
|
Observa la
gráfica de la función. Podemos comprobar que
f’’(x)>0 en
(- Como la
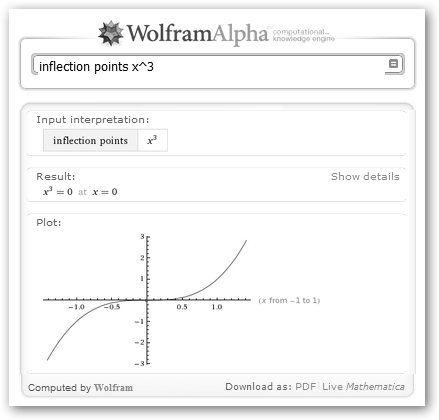
concavidad cambia tanto en Un ejemplo sencillito es x3. (x3)’’=6*x. Para x>0, (x3)’’>0 es convexa (similar en forma a x2); para x<0, (x3)’’<0, es cóncava y, en consecuencia x=0 es un punto de inflexión. |
|
|
Otro ejemplo
clásico es
|
|
7.4. Gnuplot, graficando sin límites
7.4.1. Instalación y primeros pasos.
|
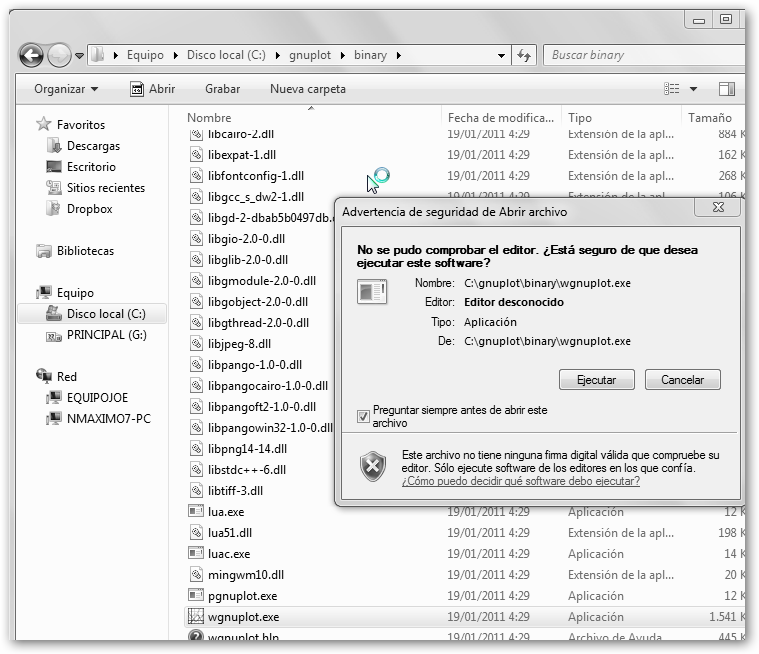
Casi todo tiene un precio, unas ventajas e inconvenientes. Gnuplot es el más potente y rápido de todas las herramientas presentadas. En su contra, es la más complicada y menos “amigable” con diferencia. En Windows navega a www.gnuplot.info y descarga la versión adecuada en la sección Download para tu sistema operativo. Descomprime el archivo zip a tu disco duro. Navega al directorio binary de la carpeta descomprimida y haz doble clic sobre wxgnuplot.exe. |
Tienes que darle permiso haciendo clic en Ejecutar. Para evitarte todo esto puedes crear un acceso directo en el escritorio. |
|
Observa la interfaz de wxgnuplot, bastante sencilla y sobria. También puedes ejecutar el archivo gnuplot.exe que es la consola gnuplot “pelada”, un poco feílla y pálida. En Ubuntu escribe en la consola: sudo apt-get install gnuplot gnuplot-doc plotdrop qgfe y te llevas de camino dos interfaces “más amigables”: plotdrop y qgfe.
|
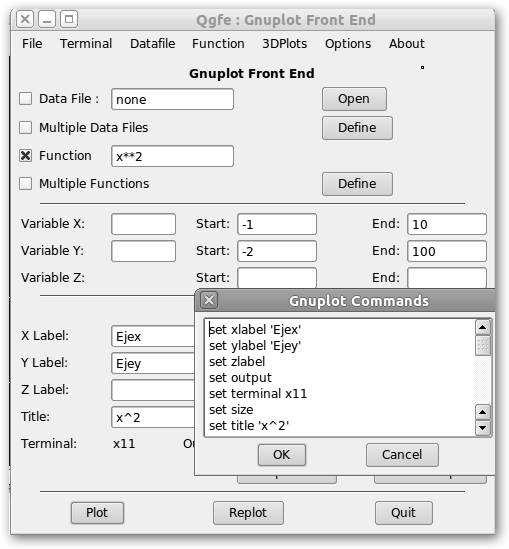
Fíjate en la interfaz de qgfe, configura las opciones y pulsa el botón Plot. Te muestra una ventana titulada Gnuplot Commands donde te indica las órdenes de Gnuplot que has especificado desde su interfaz y te muestra la gráfica (en el ejemplo x2). |
|
Nosotros nos vamos a olvidar de interfaces gráficas
“blandengues” y lo vamos a hacer directamente desde
consola “a lo vivo”, sin anestesia
1. Para iniciarlo en GNU/Linux escribe en el terminal gnuplot. |
|
|
2. A continuación,
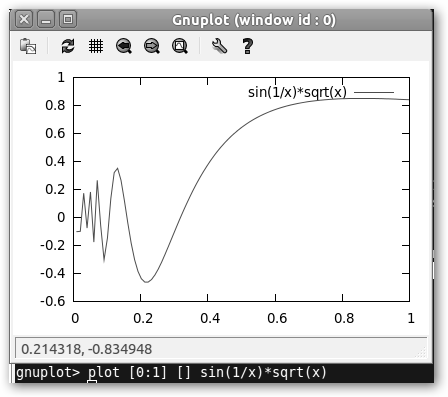
dibujamos una función “sencillita”
|
|
|
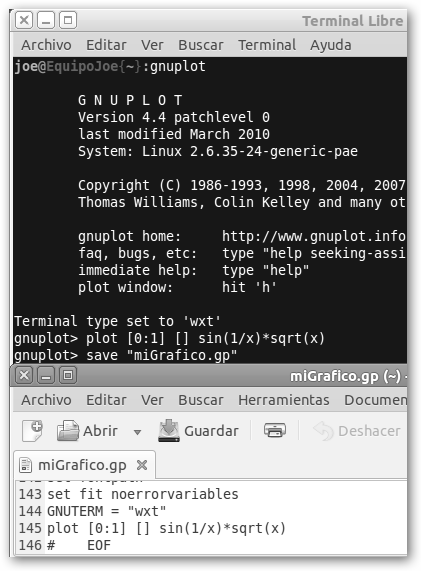
Observa la instrucción plot [0:1] [] sin(1/x)*sqrt(x), hemos especificado que el rango de las x esté entre 0 y 1, el de las y se lo dejamos a gnuplot que se “busque la vida como Orzowey”. El resultado es muchísimo mejor. |
¡Menudo invento! ¡Qué churro! Bueno… Vamos a mejorarlo, ya sabes: “la paciencia es la madre de la ciencia”.
|
Elementos que te serán muy útiles:
* ¿Cómo salir? exit, quit o las teclas Ctrl+D.
* Ayuda: help, luego tendrás que elegir un Topic o tema o directamente help orden. En Windows Vista y 7 necesitarás instalar Windows Help program del centro de descargas, www.microsoft.com/downloads.
* Histórico de órdenes: con las teclas del cursor puedes acceder a órdenes previas, es decir, gnuplot guarda un histórico de comandos.
7.4.2. Dibujando archivos de datos.
|
1990 2.350.000 1991 2.289.000 1992 2.259.900 1993 2.537.900 1994 2.647.000 1995 2.449.000 1996 2.275.400 1997 2.118.700 1998 1.785.700 1999 1.613.700 2000 1.556.400 2001 2.069.563 2002 2.049.607 2003 2.096.887 2004 2.113.718 2005 2.069.854 2006 2.039.414 2007 2.039.054 2008 2.539.941 2009 3.644.041 2010 4.060.756 |
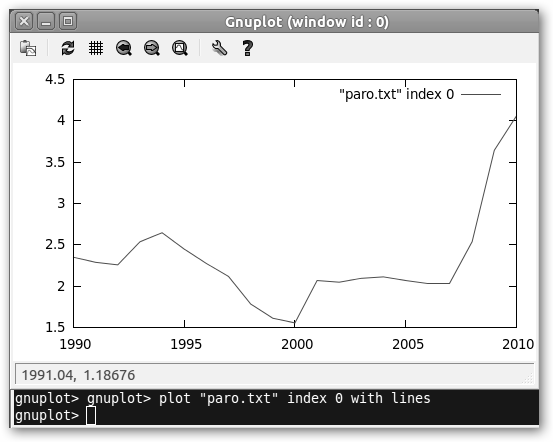
Supongamos que queremos graficar un conjunto de datos. Estos corresponden a las tasas de paro en España desde 1990 hasta el 2010 (no aseguro que sean fiables, ¿alguien podría?).
|
|
|
La
instrucción es plot “paro.txt” index 0 using 1:2 with
lines, desmenucémosla
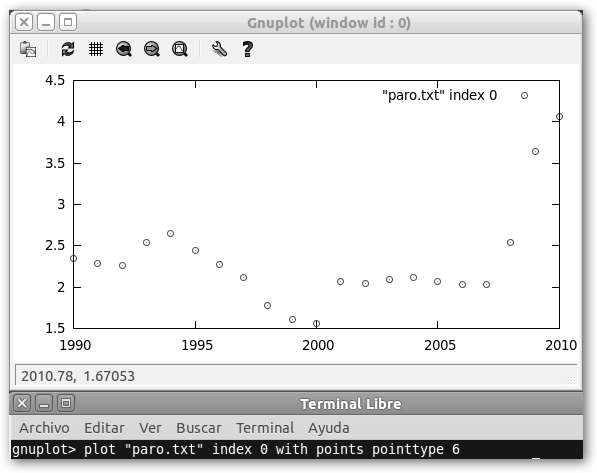
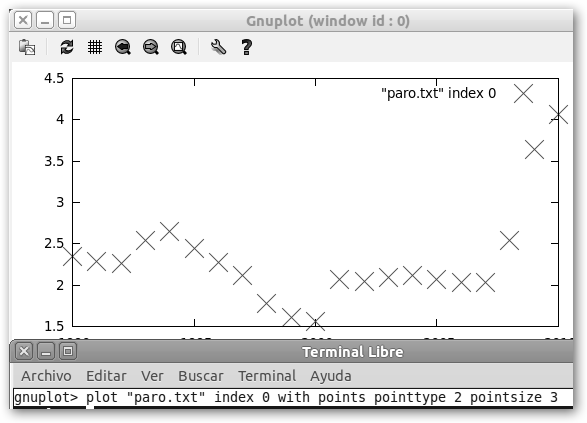
* plot “paro.txt”: dibuje los datos del fichero paro.txt * index 0: para gnuplot los ficheros se dividen en conjuntos de datos divididos por dos líneas en blanco. En nuestro caso, solo tenemos un conjunto de datos y como gnuplot empieza a contar en 0, index 0 apunta al primero (observa que index 1 apuntaría al segundo, index 2 al tercero y así sucesivamente). Podría utilizarse con esta sintaxis index primerConjunto:últimoConjunto:incremento, por ejemplo index 2:8:2 graficaría los siguientes conjuntos de datos: 2, 4, 6 y 8. * with lines: indica el estilo. En la figura inferior izquierda indicamos que queremos graficar los datos con puntos de tipo 6 (with points pointtype 6) y en el derecho con puntos de tipo 2 y tamaño 3 (with points pointtype 2 pointsize 3). |
||
|
|
|
|
7.4.3. “Como un pro”: creando scripts, afinando nuestros gráficos y exportando los resultados a imágenes.
|
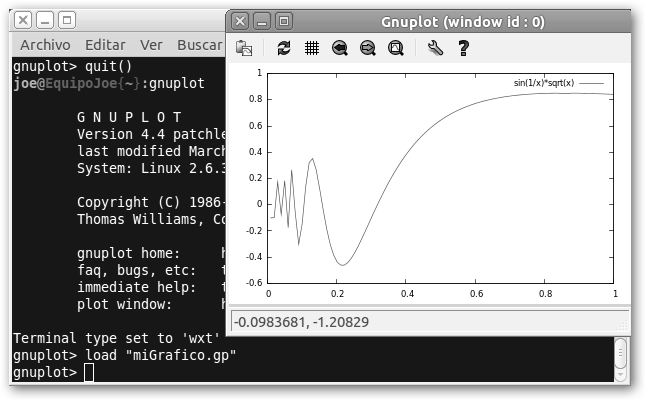
Si queremos afinar nuestro trabajo y vamos a dedicarle tiempo, mejor será que lo guardemos y no lo perdamos. Por tanto, cuando hayas acabado teclea save “miGrafico.gp” y te creará un fichero con todas las órdenes que hayas escrito y muchas, muchas más… ¿Si yo sólo había escrito la 145? Observa el fichero miGrafico.gp abierto con un editor de textos justo debajo del terminal. Para recuperar el trabajo teclea load “miGrafico.gp” y “disfruta” de nuevo de nuestra gráfica. Otra opción es crear el fichero con extensión gp con nuestro editor favorito y copiar y pegar las instrucciones que consideremos pertinentes. Esto tiene la gran ventaja de no tener un script “apabullante” que para empezar tiene 146 líneas y una sola nuestra. Vamos a hacer nuestro propio script, recuerda siempre con extensión gp. |
|
|
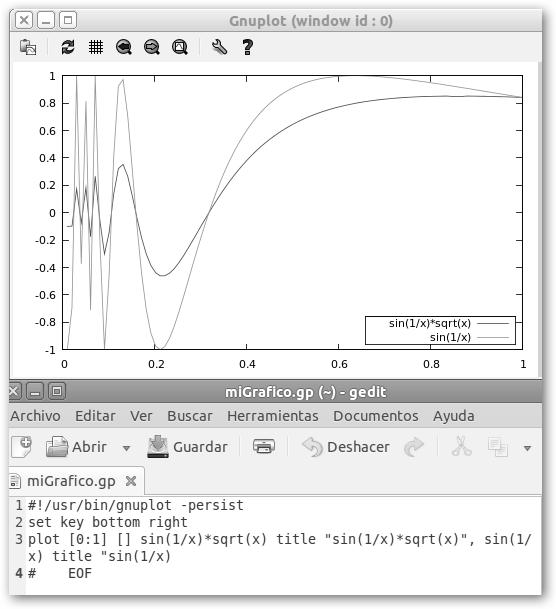
En él se ilustra en la línea 2 cómo crear una leyenda con set key botton right, por supuesto puedes crearlo arriba (top), a la izquierda (left) o centrado (center). Además, observa que hemos graficado dos funciones (separadas por comas) cada una tiene su propio título definido con tittle en el que hemos indicado de qué función se trata. |
Comprueba que hemos eliminado casi todas las líneas del fichero miGrafico.gp. |
|
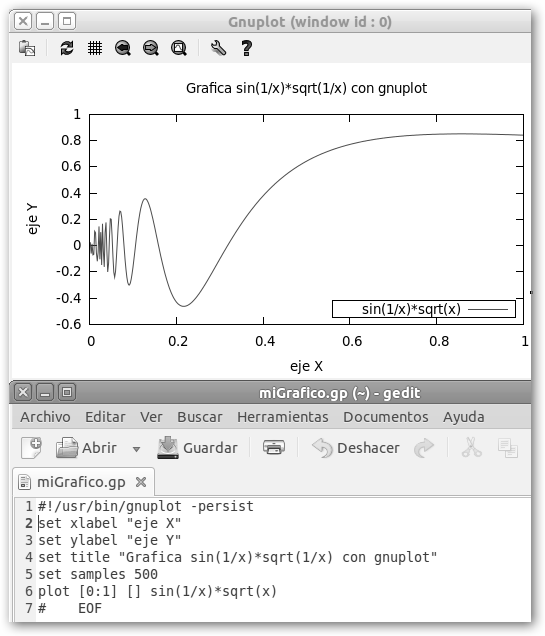
Veamos cómo podemos mejorar el gráfico original con varias órdenes: 1. set xlabel, set ylabel especifican las etiquetas de los ejes X e Y. 2. set tittle: asignamos un título al gráfico. 3. set samples 500: indicamos que queremos que se evalúen 500 puntos para graficar la función. Observa que hay un mayor nivel de detalle. Mostramos en la figura inferior como exportar nuestros gráficos a imágenes: |
|
4. set term jpeg y set output "miGrafica.jpeg" especificamos el formato y el archivo donde se almacenará la gráfica.
5. set encoding iso_8859_1: nos permite incluir acentos, observa que en el título ahora Gráfica lo lleva.
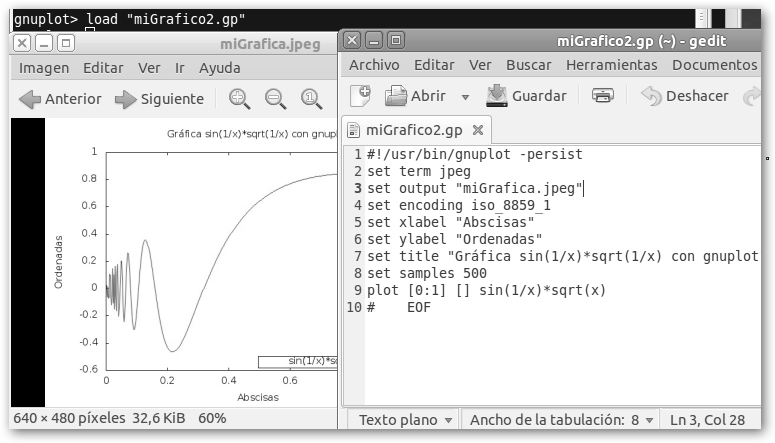
Fíjate en el detalle del archivo gráfico miGrafica.jpeg obtenido al ejecutar el script (load “miGrafico2.gp”). ¡Recuerda volver a los valores originales con set terminal x11 y set output!, es decir, que muestre las imágenes por pantalla no en archivos gráficos.
7.5. Mira mamá: “funciones en 3D”.
|
¿Quieres impresionar a mamá con la función
volcán Requerimos que
dibuje la función
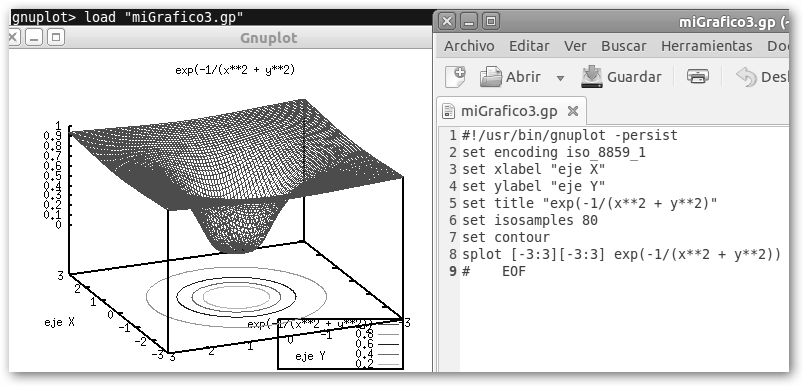
A continuación, mostramos cómo realizar gráficas 3D en gnuplot. Lo haremos con un script como ya hemos aprendido. |
|
|
|
|
La orden básica es
splot [-3:3][-3:3] exp(-1/(x**2 + y**2)). Indicamos que grafique
![]() con “x” e “y” tomando valores en el intervalo
[-3, 3]. Con set isosamples 80 aumentamos la resolución (a precio de
ralentizar el proceso) y con set contour activamos las líneas de contorno
en la base de la imagen.
con “x” e “y” tomando valores en el intervalo
[-3, 3]. Con set isosamples 80 aumentamos la resolución (a precio de
ralentizar el proceso) y con set contour activamos las líneas de contorno
en la base de la imagen.
|
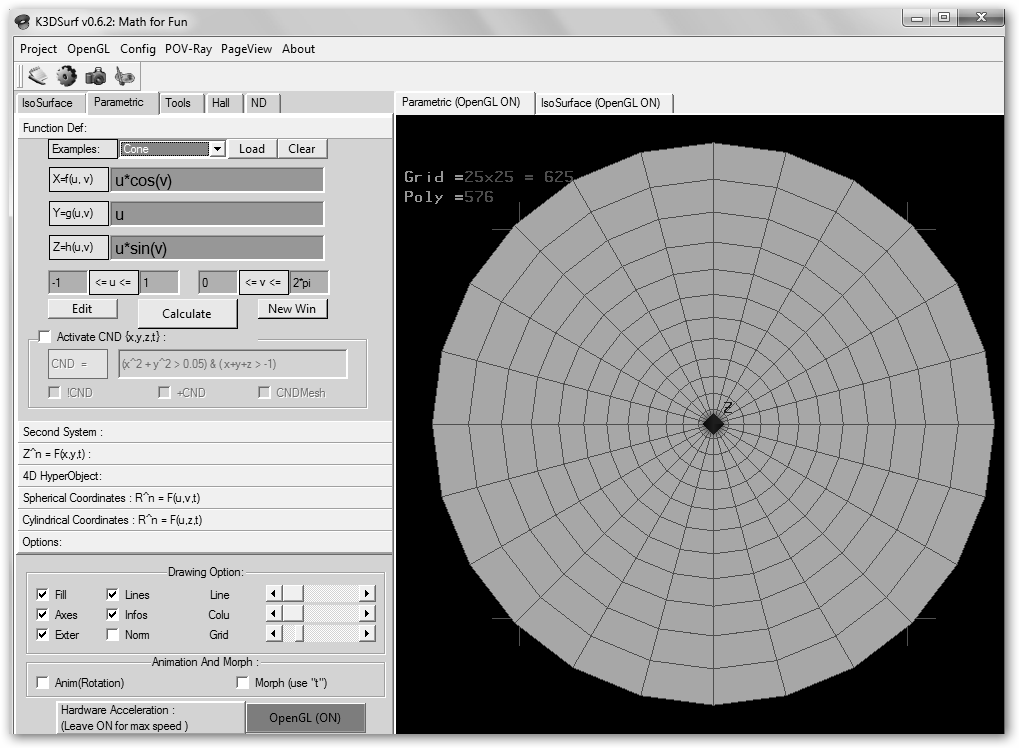
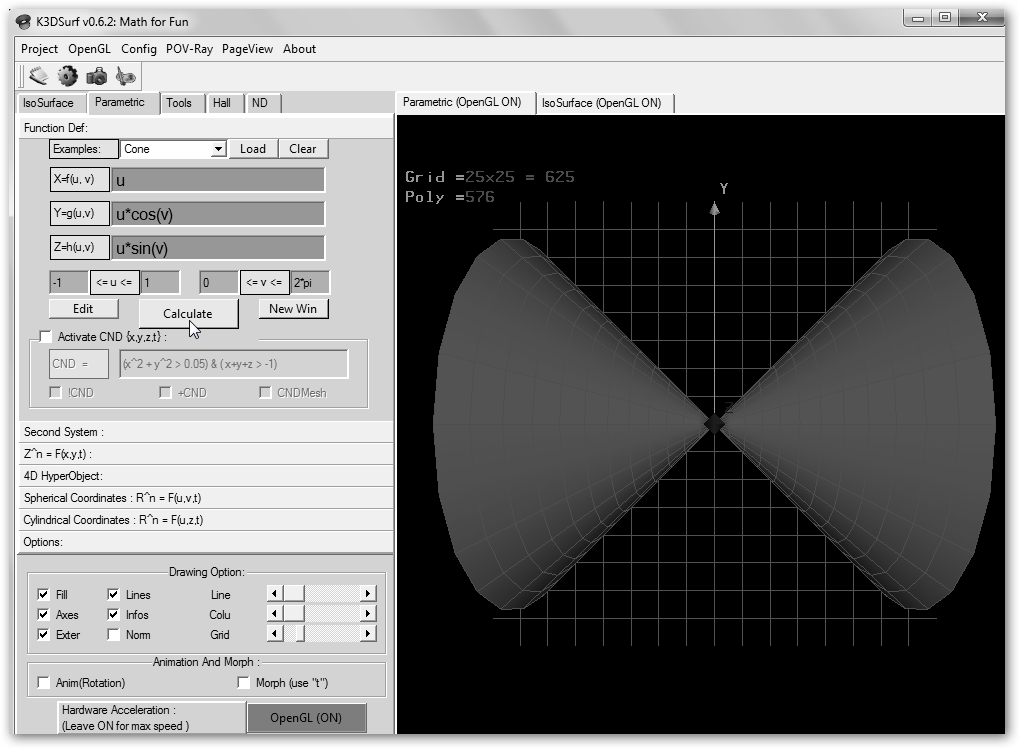
Si no quieres complicarte tanto la vida puedes utilizar la galería de más de 50 ejemplos de K3DSurf Math for fun en k3dsurf.sourceforge.net . En Ubuntu instala k3dsurf. Además, las superficies puedes animarlas seleccionando Anim(Rotation) y moverlas o rotarlas a clic de ratón.
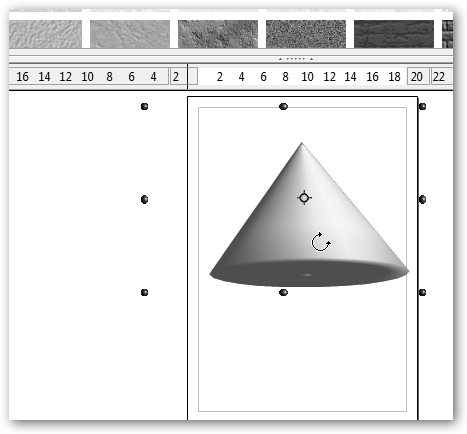
¿Y esto es un cono? Claro que sí, pero vamos a cambiar el eje de revolución editando directamente la ecuación tal como se ilustra. Haz clic en Calculate para ver el resultado. |
|
|
|
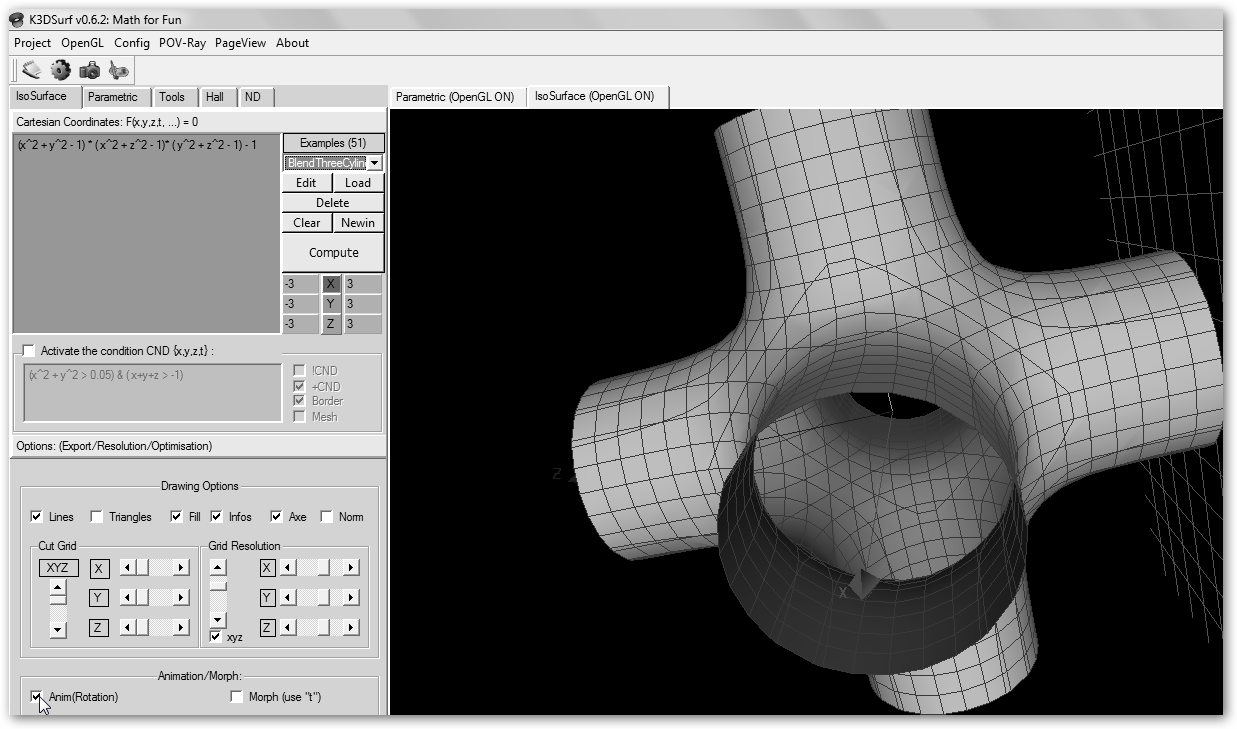
¡De eso se trata! Modifica las ecuaciones, define tus propias funciones, experimenta, aprende,… |
||
|
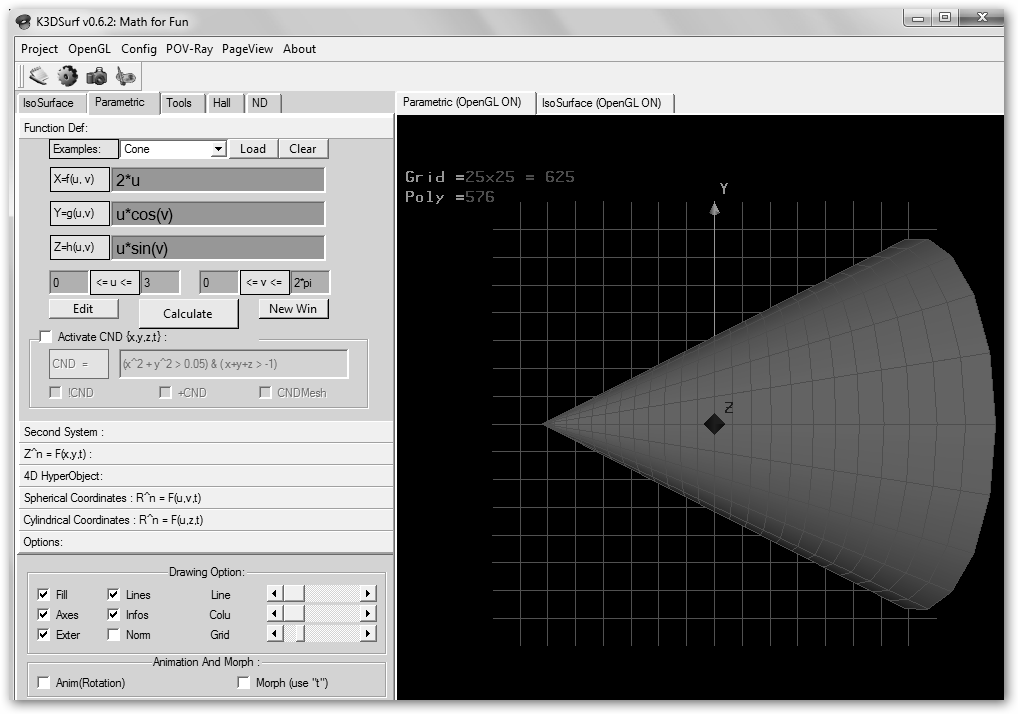
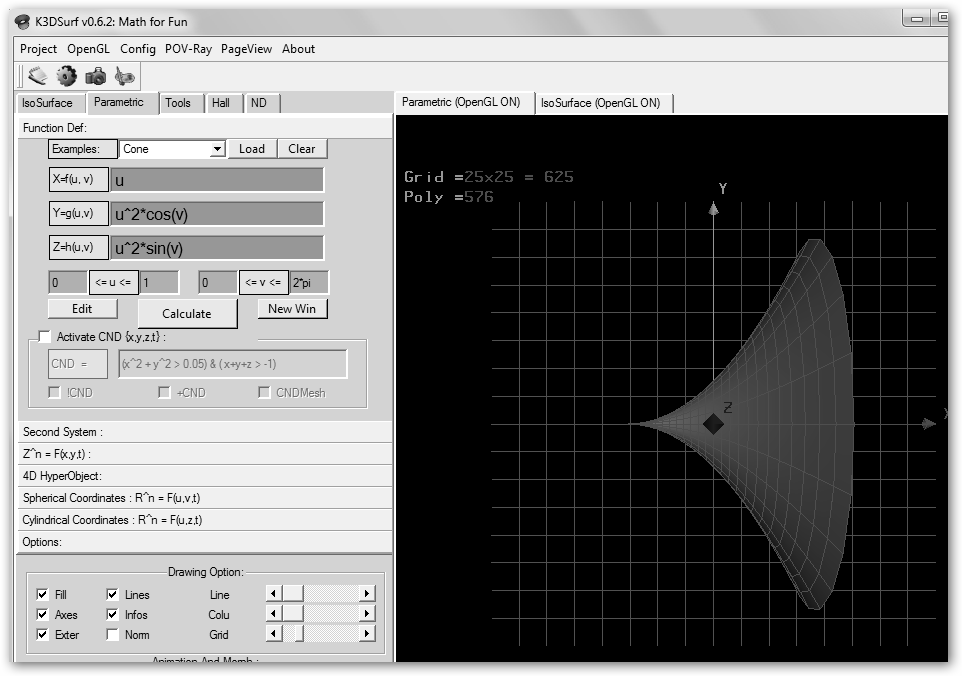
Haz que “u” varíe entre [0, 3] y verás un único cono. Cambia x por x=2*u y tendrás un cono más alargado; haz lo propio con y= 0.5*u*cos(v), z= 0.5*u*sin(v) y lo tendrás más estrecho. Observa como demostración final que hemos creado dos nuevas funciones. La primera, por ejemplo, es un arco de parábola rotando alrededor del eje X. |
|
|
|
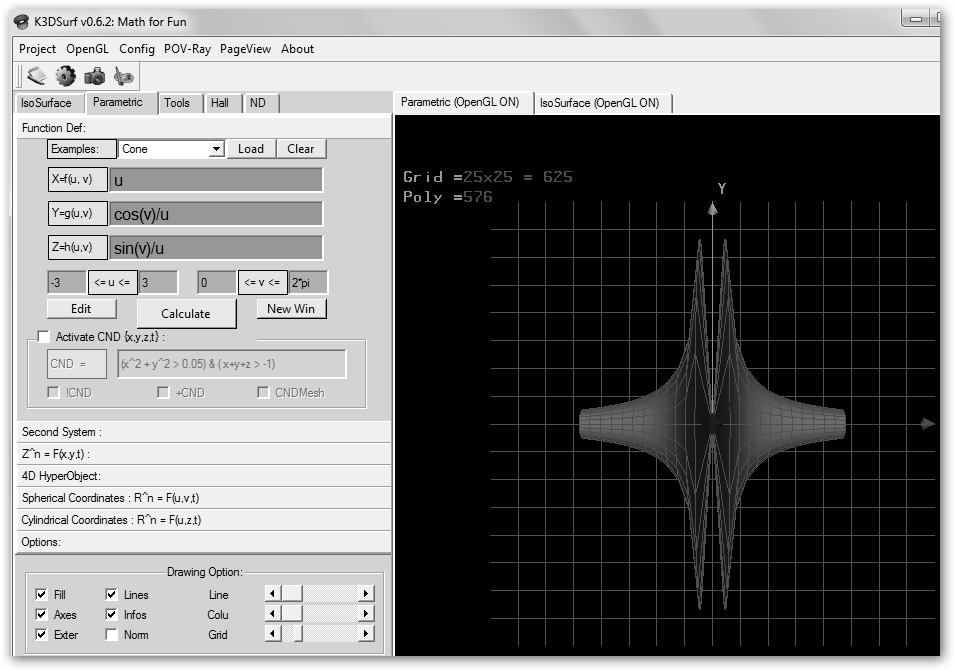
Sustituye u2 por sqrt(u) en Y, Z y tendrás una campana. |
|
|
7.6. Geometría del espacio.
|
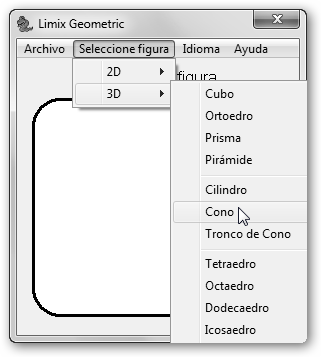
La herramienta más sencilla para explorar figuras geométricas en el espacio es Limix Geometric. Su página web es www.limix.net navega por Nuestros programas, Limix Geometric y podrás obtenerlo gratuitamente, sin límites de uso. |
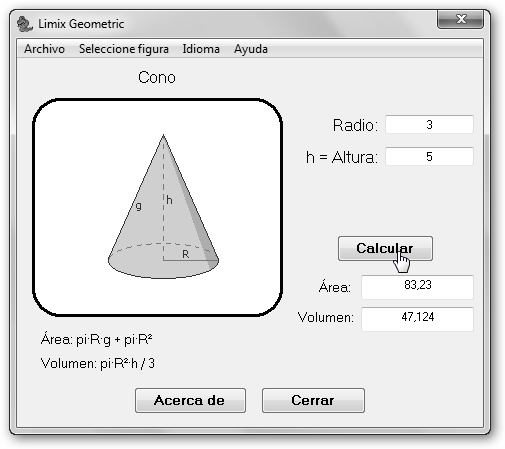
Basta con descomprimirlo y ejecutarlo, no presenta un asistente de instalación. Selecciona una figura 3D (Cubo, Ortoedro, Prisma, Pirámide, etc.) desde Seleccione figura, 3D, en la figura se ha seleccionado Cono. Indica los datos (en este ejemplo Radio y Altura) y haz clic en Calcular. Obtendrás el área y el volumen, así como, las fórmulas con las que se obtuvieron. |
|
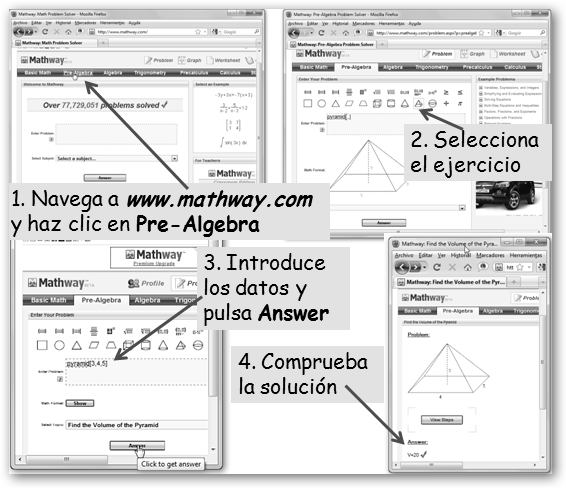
Una propuesta en la misma línea pero en Internet y en inglés, la puedes encontrar en Mathway.
|
|
|
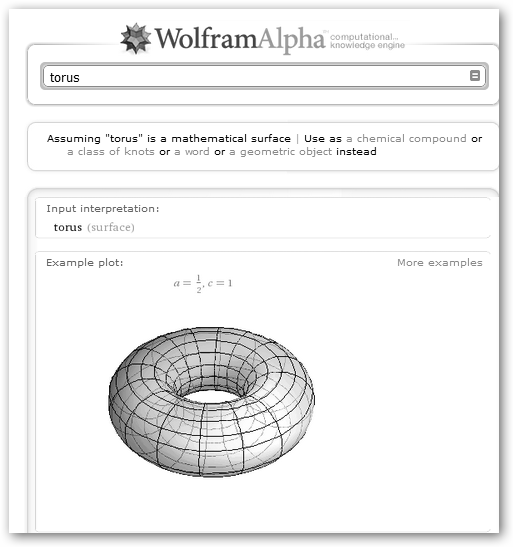
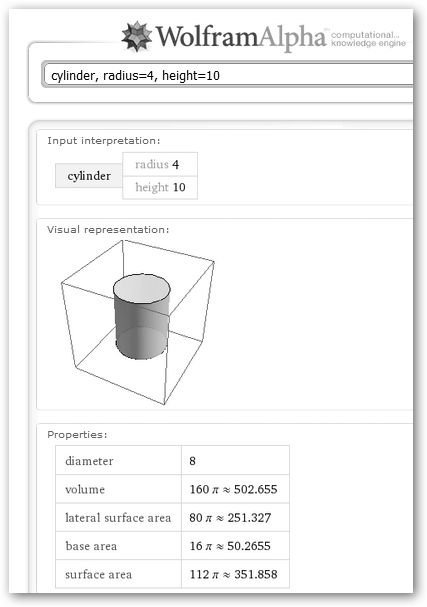
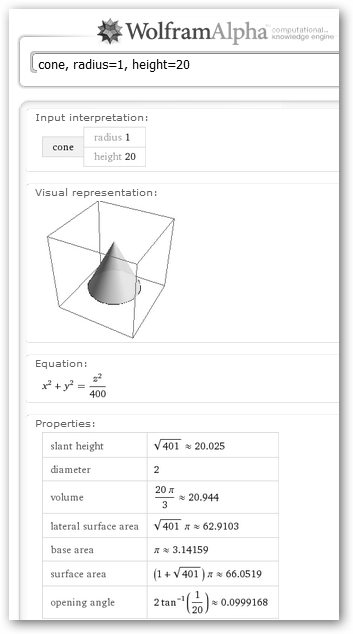
En Wolfram Alpha podemos explorar todo tipo de figuras geométricas (torus, sphere, cylinder, square pyramid, pentagonal pyramid, platonic solid) y conocer sus ecuaciones cartesianas y paramétricas, volúmenes, etc. |
Detalle de la continuación de la respuesta de Wolfram a la petición anterior. |
|
Observa que indicamos a Wolfram el radio y la altura tanto de un cilindro como de un cono y obtenemos el diámetro, su volumen, el área de la base, etc. |
|
|
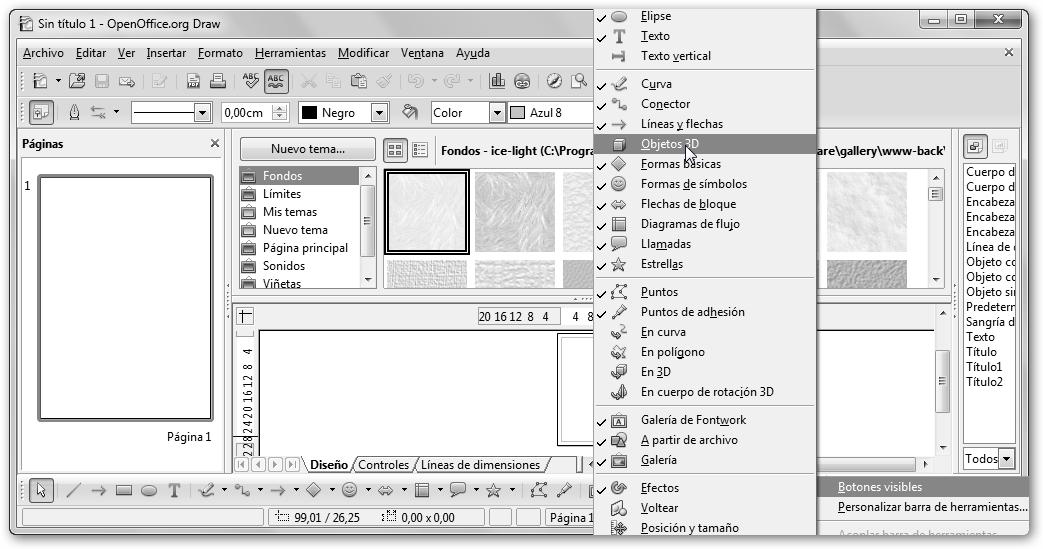
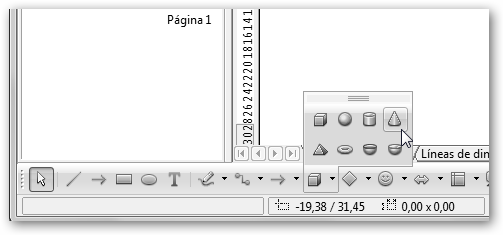
Si quieres dibujar las figuras geométricas básicas, moverlas, aplicarles texturas, etc. tu aplicación es OpenOffice.org Draw de la suite OpenOffice (www.openoffice.org). Arráncalo desde Inicio, Todos los programas, OpenOffice.org 3.1, OpenOffice.org Draw. A continuación, tendrás que habilitar un nuevo botón en el panel inferior derecho: ↓, Botones visibles, Objeto 3D. |
|
|
Confirma que aparece el nuevo botón Objeto 3D en el panel inferior. Con el podrás dibujar las figuras geométricas más importantes: cubo, esfera, cilindro, cono, etc. Una vez dibujadas podrás moverlas, modificarlas, por ejemplo, cambiarle la iluminación, la textura o el material (haz clic en la figura con el botón derecho y selecciona Efectos 3D), etc. |
Si quieres algo más, precisarás Google ScketchUp (sketchup.google.com/intl/es/). Es un programa de diseño y modelado 3D pensado para ser sencillo de utilizar. |
|
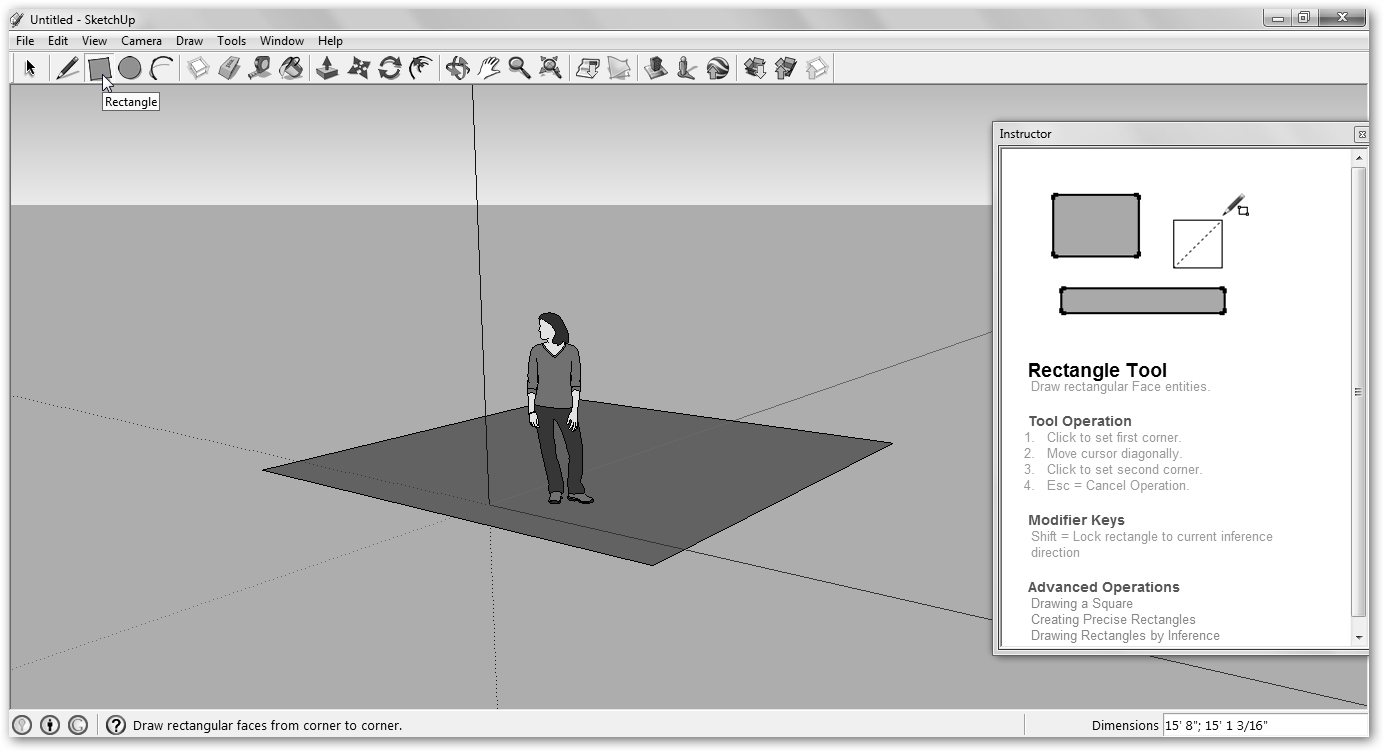
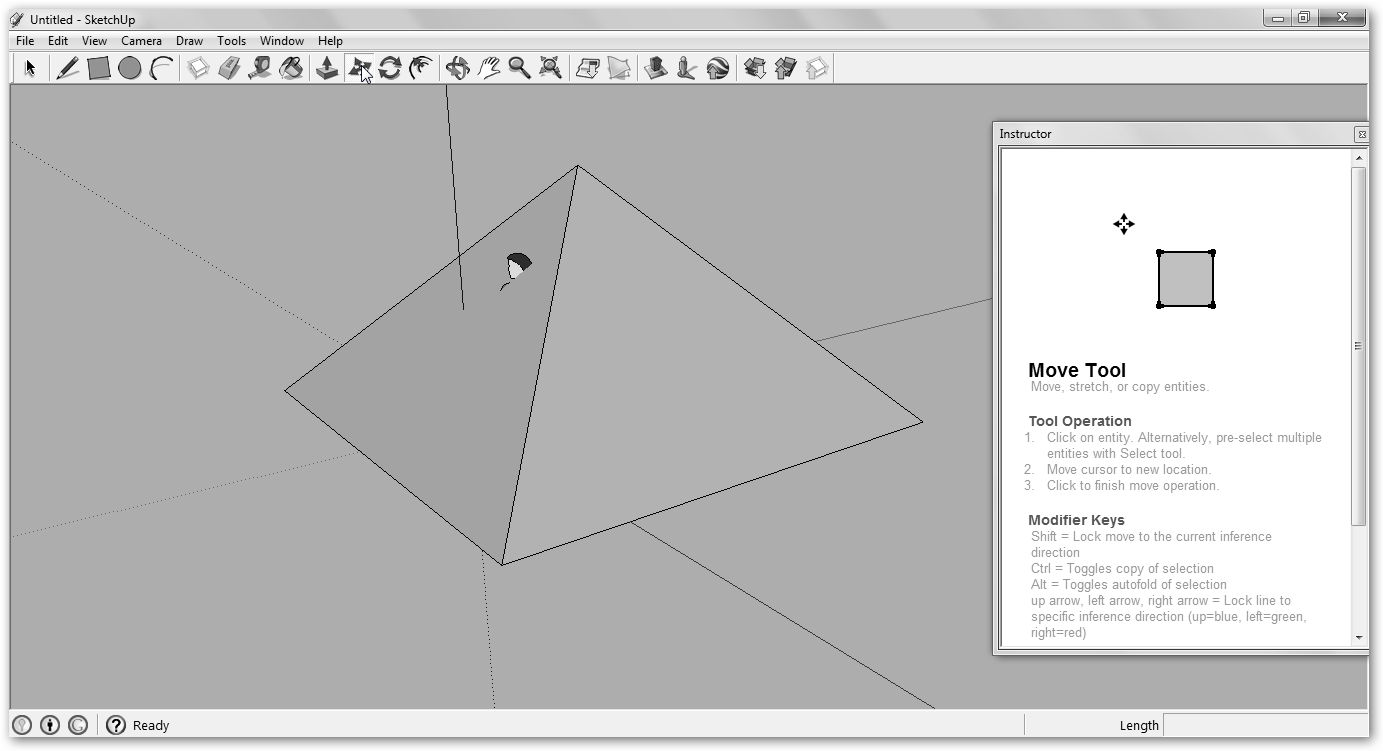
Vamos a construir una pirámide. Descarga e inicia el programa: Inicio, Todos los programas, Google ScketchUp 8, Google ScketchUp 8. Pulsa en Start using SketchUp para evitar los tutoriales, diferentes enlaces y demás y empezar a utilizar la aplicación. |
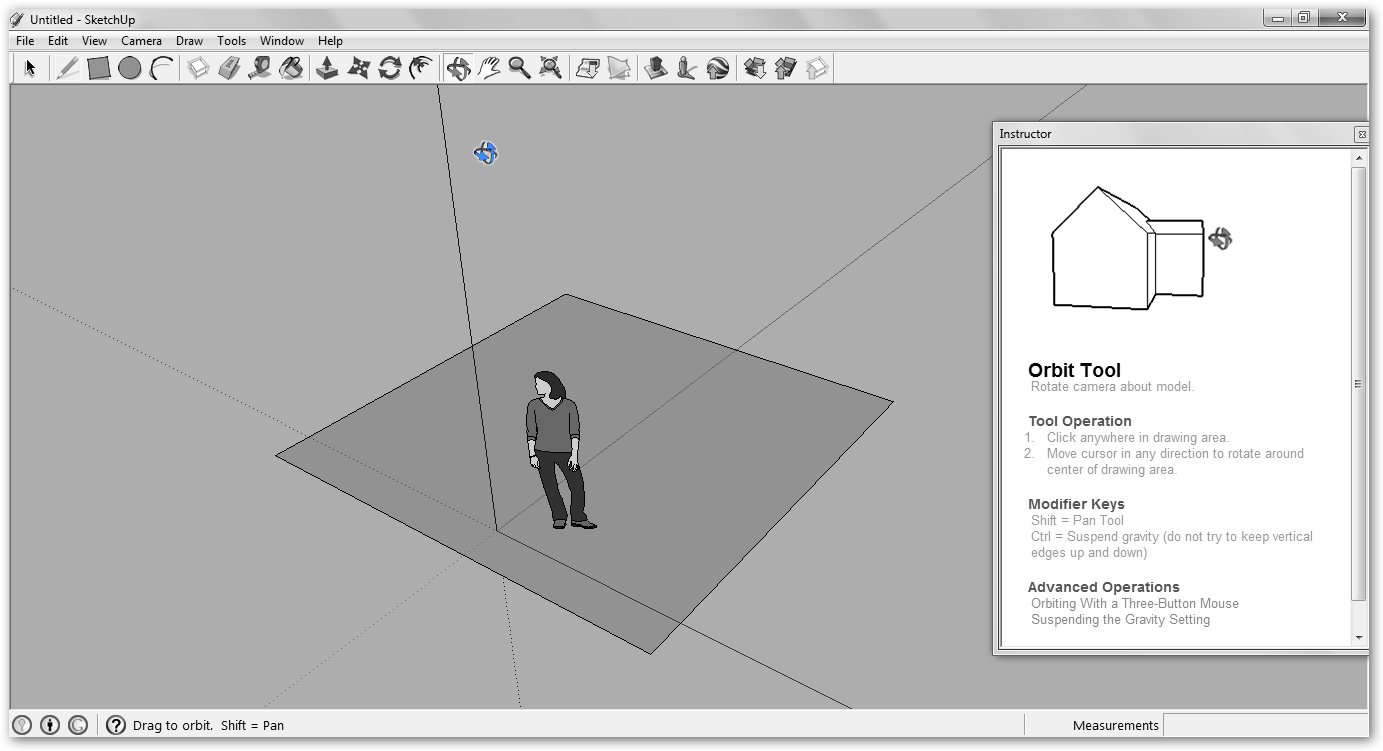
Con la herramienta Rectangle, Rectángulo dibuja la base de nuestra pirámide. A continuación, vamos a movernos por el dibujo con la opción Orbit para trabajar más cómodamente. |
|
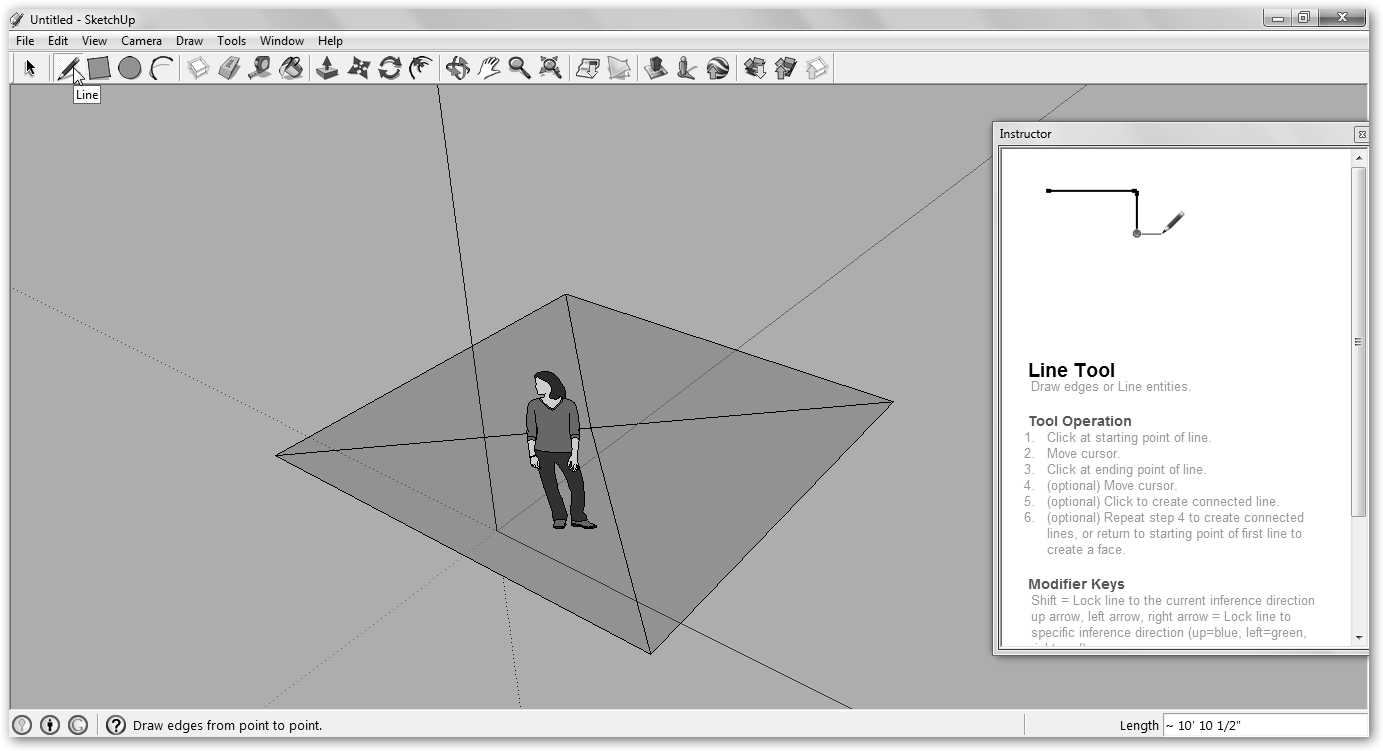
Dibujamos lo que será la cúspide de la pirámide en el medio y lo unimos con los vértices de la base con Line (línea). Primero unimos dos vértices, luego de un tercero trazamos una línea al punto medio (MidPoint) y de éste al cuarto. |
Con la herramienta Move subimos la cúspide o el ápice de nuestra pirámide haciendo clic sobre él. Si te molesta el personaje, selecciónalo y con el botón contextual haz clic en Erase, borra. |
|
|
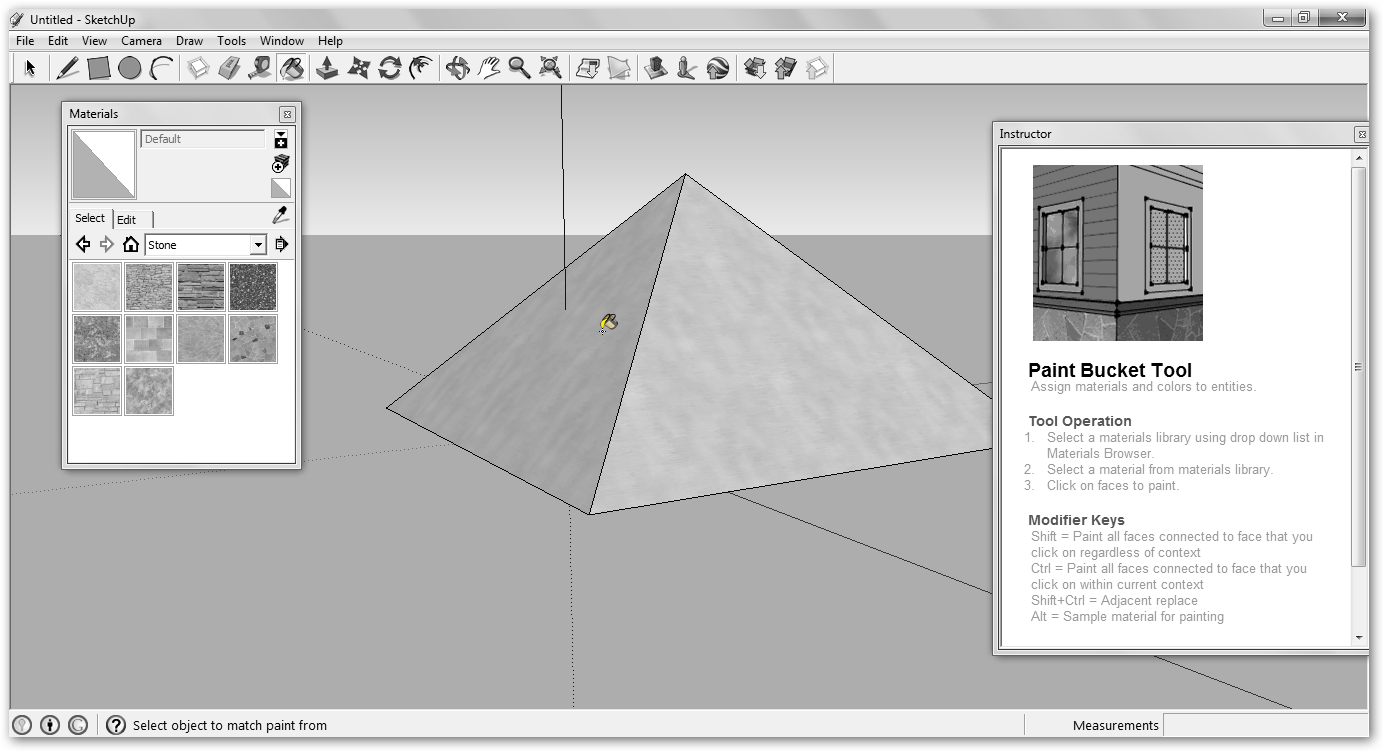
Ahora podemos decorarlo utilizando Paint Bucket, crear nuevos objetos, girarlos con Orbit, rotarlos (Rotate), moverlos (Move), cambiar la posición de la cámara, importarlos desde la galería sketchup.google.com/3dwarehouse o con Get Models…, etc. Una alternativa más difícil de utilizar es Blender, www.blender.org. |
|
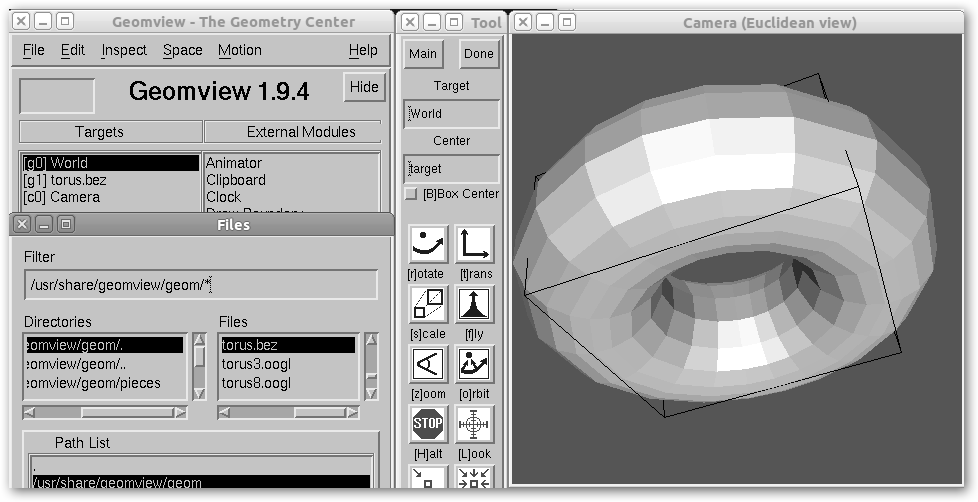
Otra posibilidad para GNU/Linux es Geomview. En Ubuntu instala el paquete geomview y podrás jugar con figuras en 3D. Una vez lanzado observa cómo se ha abierto un toro desde File, Open buscándolo en su catálogo en /usr/share/geomview/geom; luego podrás rotarlo, trasladarlo, escalarlo, … Una página web “a consultar” es www.learner.org/interactives/ geometry/index.html. |
|
7.7. Un mar de posibilidades
Hemos recorrido en este capítulo un largo camino y visto múltiples herramientas y soluciones para graficar.
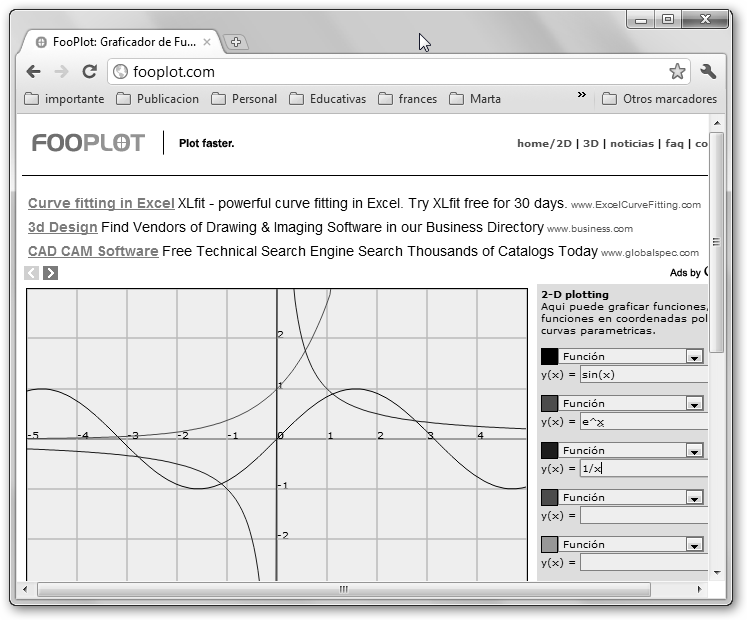
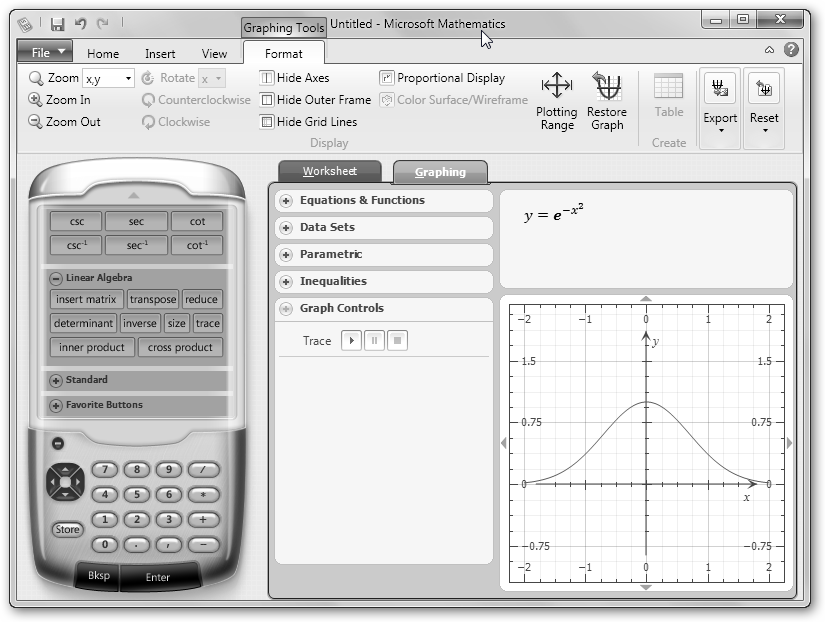
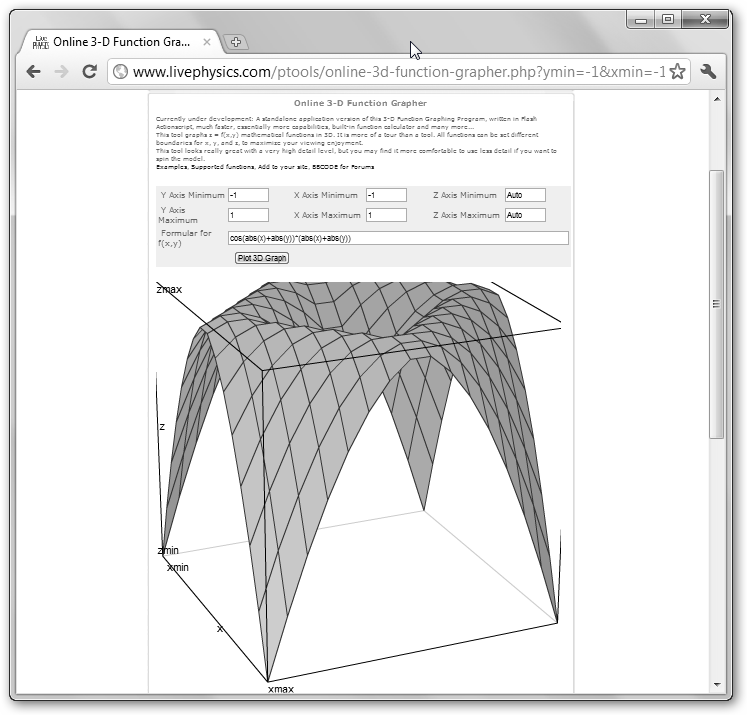
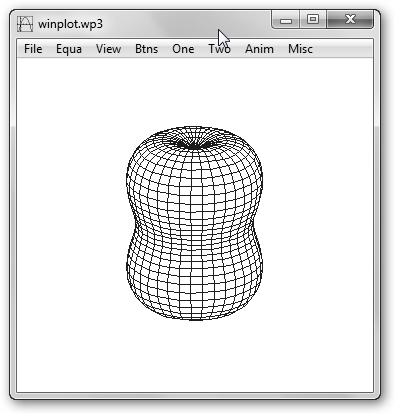
Sin embargo, hay muchas más posibilidades. Algunas son online como FooPlot (fooplot.com), CHARTPART (chartpart.com), NCES Kid’s Zone(nces.ed.gov/nceskids/, en Graph) e Interactive Physics Tools (www.livephysics.com/ptools/, sección 3D Function Grapher) y otras son aplicaciones de escritorio como SpaceTime (www.spacetime.us), Microsoft Mathematics, QtiPlot (soft.proindependent.com/qtiplot.html) y WinPlot (math.exeter.edu/rparris/winplot.html). Se muestran a continuación, a modo de mera ilustración, varias de ellas: FooPlot, Microsoft Mathematics, Interactive Physics Tools y WinPlot.
|
|
|
|
|
|
 , desde el menú Ejecutar, la opción Ejecutar
o F5.
, desde el menú Ejecutar, la opción Ejecutar
o F5. ,
desde el menú Archivo, Abrir o Ctrl,
O (O es de Open, abrir).
,
desde el menú Archivo, Abrir o Ctrl,
O (O es de Open, abrir). 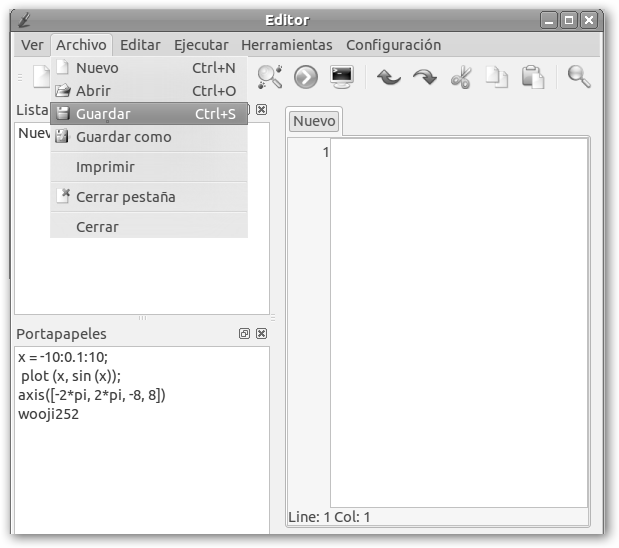
 ”
es decreciente y si se queda igual es constante.
”
es decreciente y si se queda igual es constante.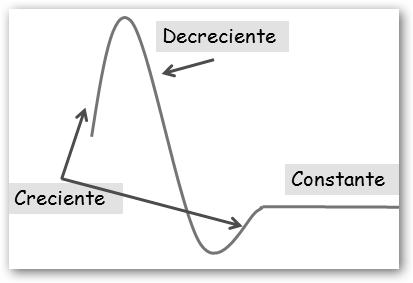
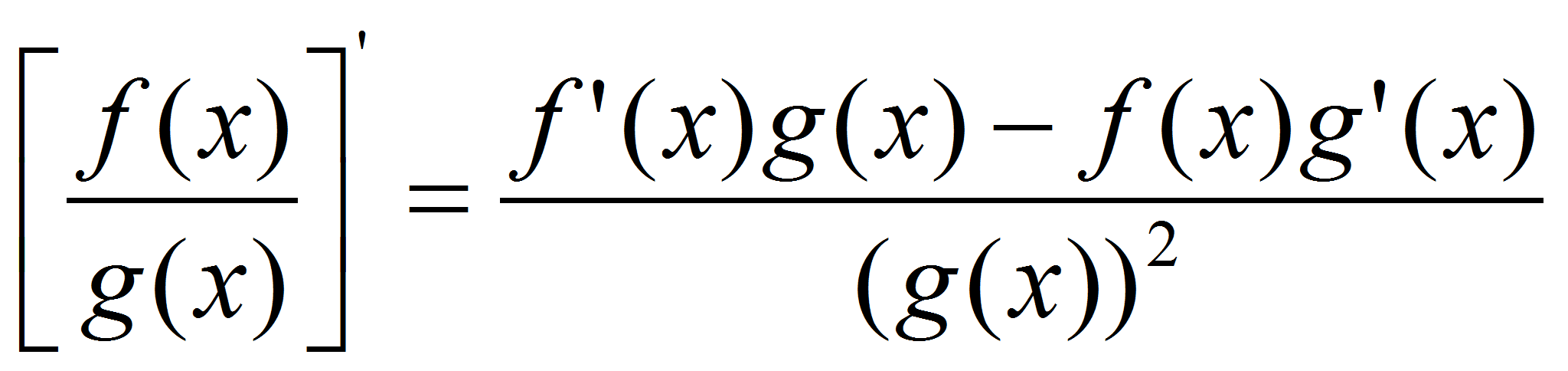
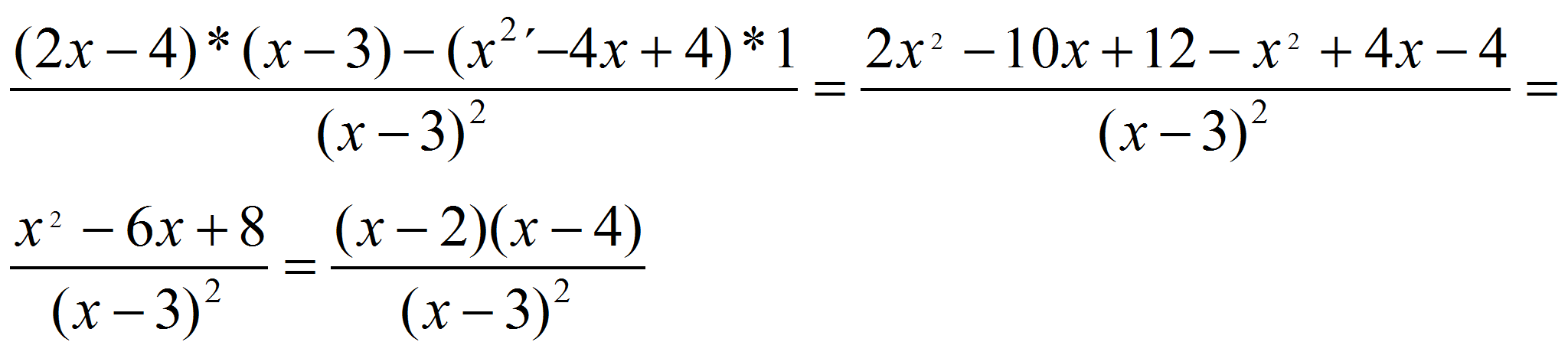
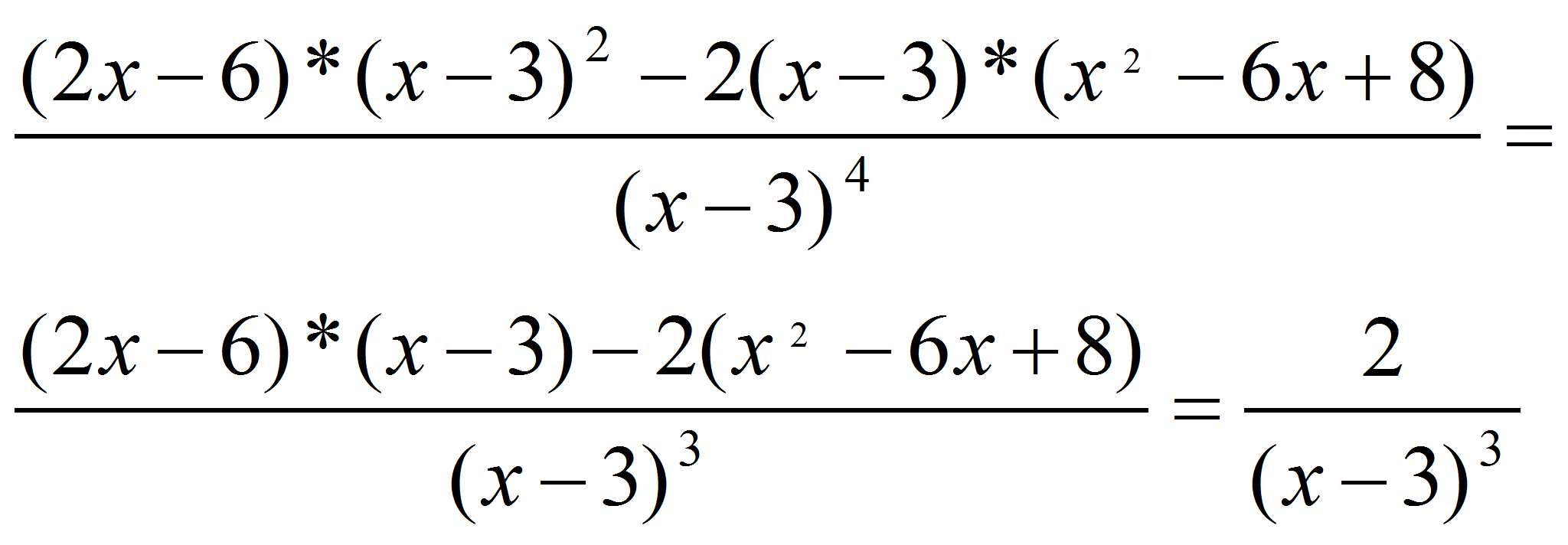

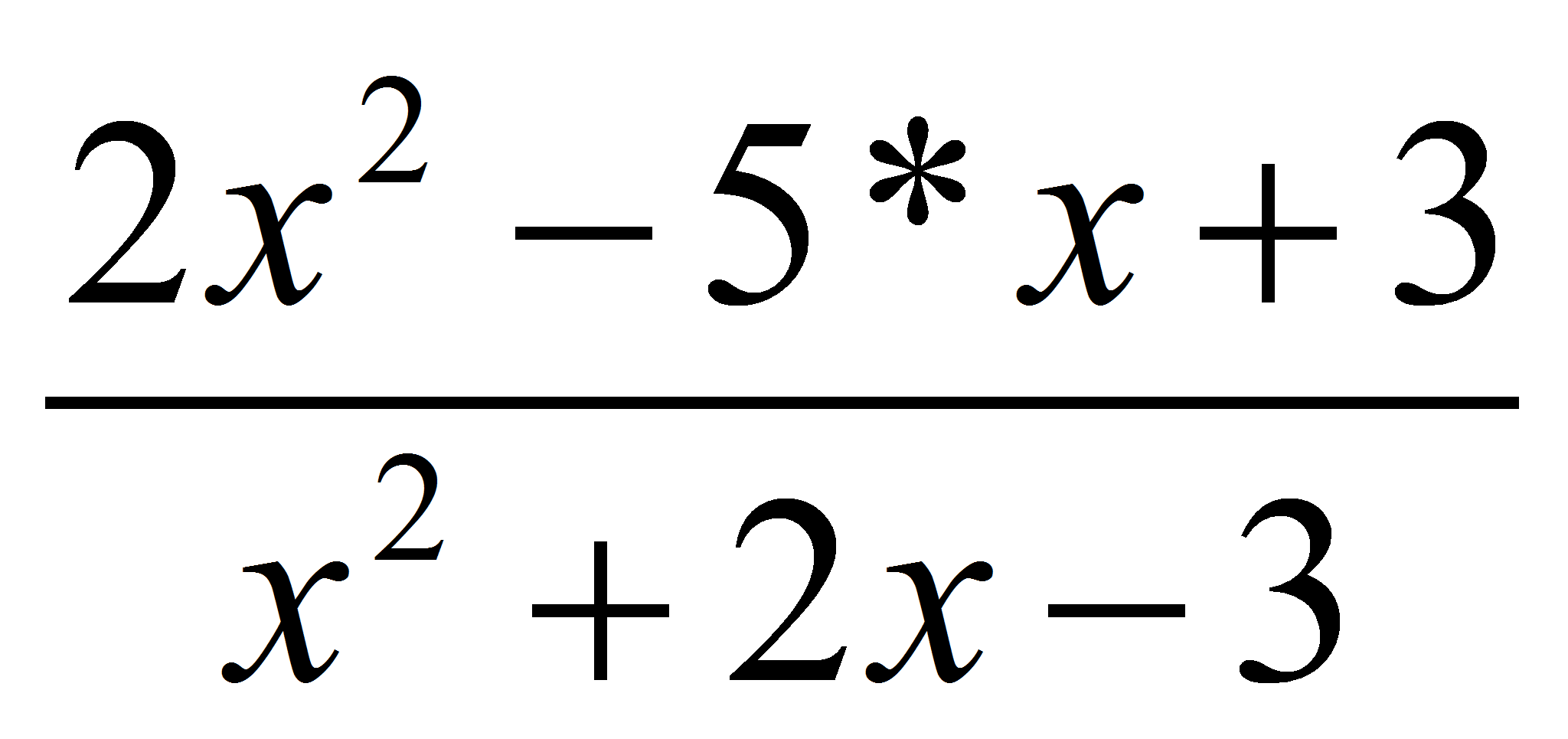 tiene una asíntota horizontal
(y=2) y otra vertical (x=3). Finalmente,
tiene una asíntota horizontal
(y=2) y otra vertical (x=3). Finalmente,
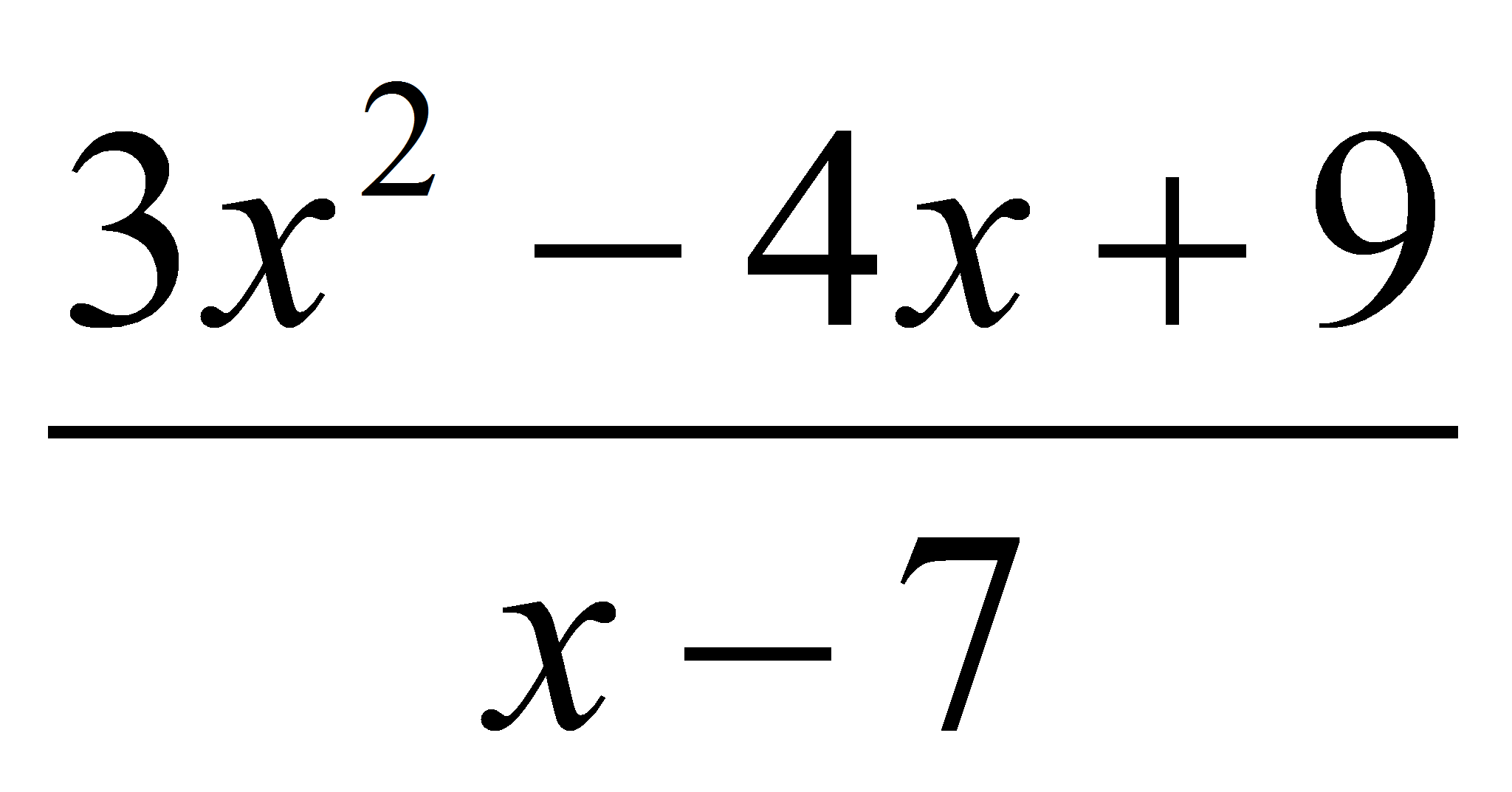 tiene una asíntota oblicua, la
recta 3x+17.
tiene una asíntota oblicua, la
recta 3x+17. 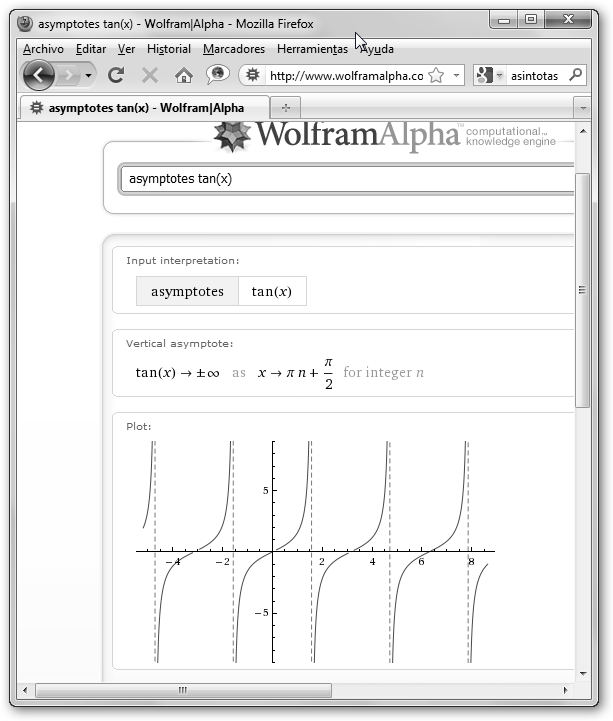
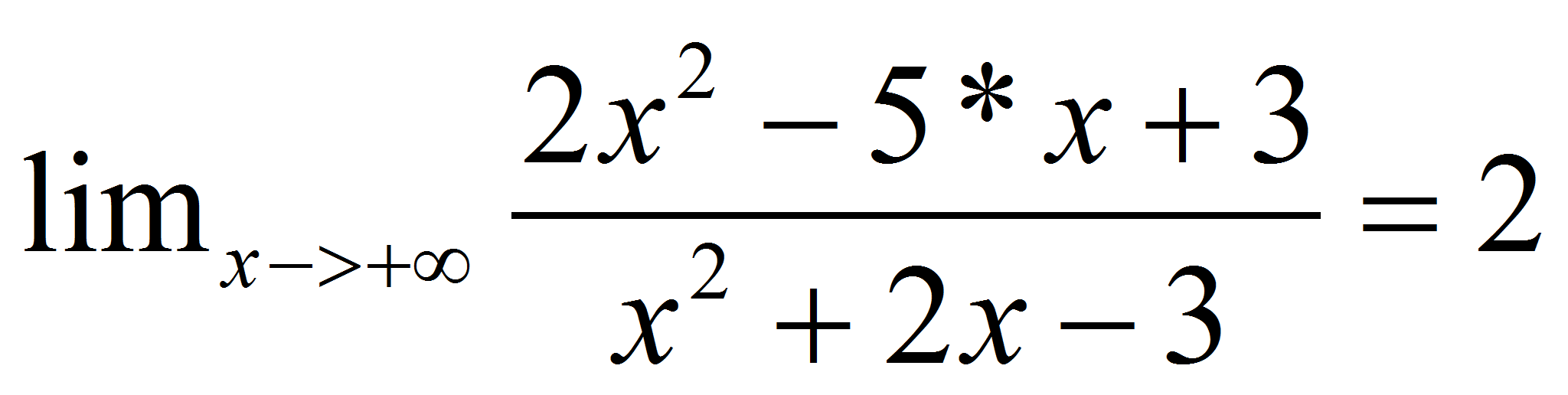 y
y
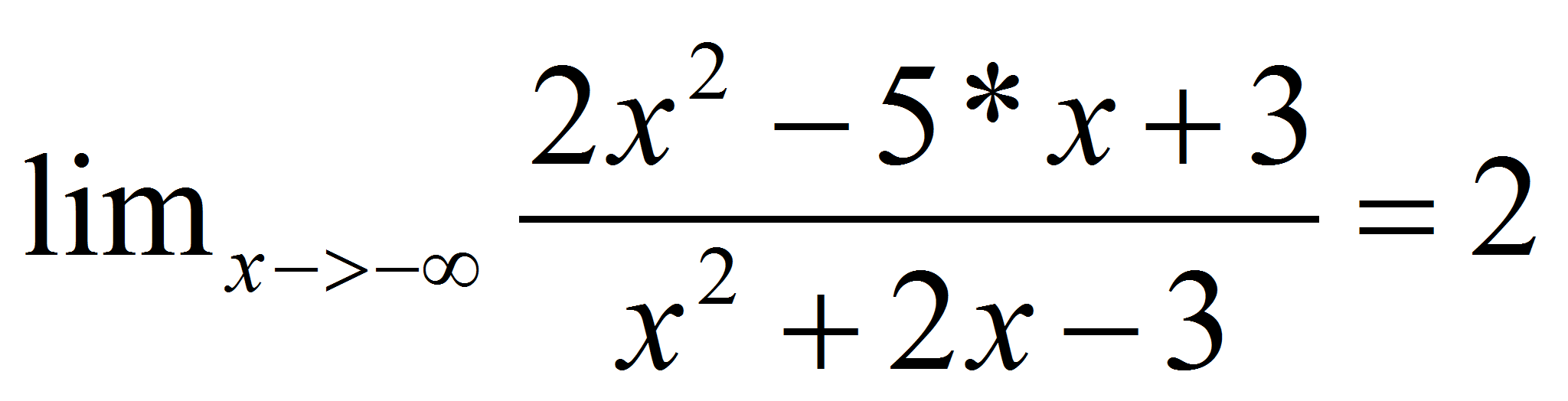 dicha
función tiene una asíntota horizontal en y=2
(conforme “x” se haga muy grande o muy pequeño,
“y” se aproximará cada vez más a 2).
dicha
función tiene una asíntota horizontal en y=2
(conforme “x” se haga muy grande o muy pequeño,
“y” se aproximará cada vez más a 2).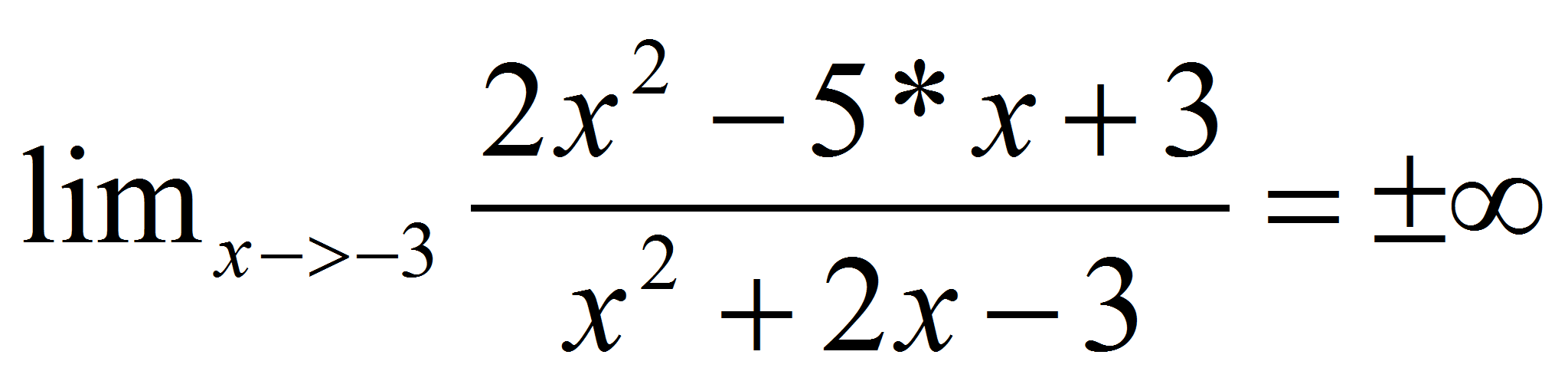 tiene una asíntota vertical en
x=-3 (conforme “x” se aproxima a 3, “y” crece
desmesuradamente).
tiene una asíntota vertical en
x=-3 (conforme “x” se aproxima a 3, “y” crece
desmesuradamente).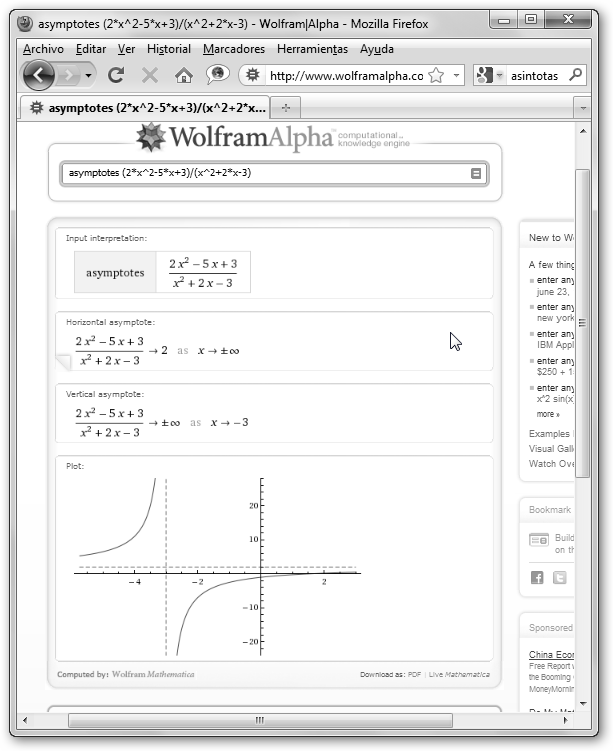
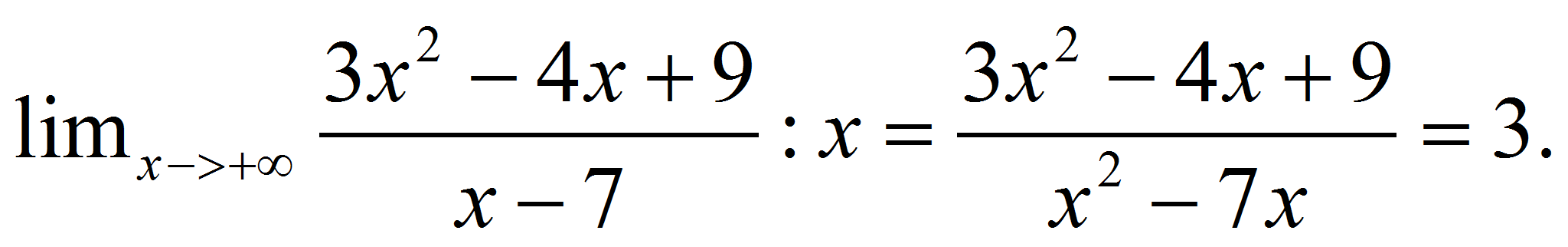
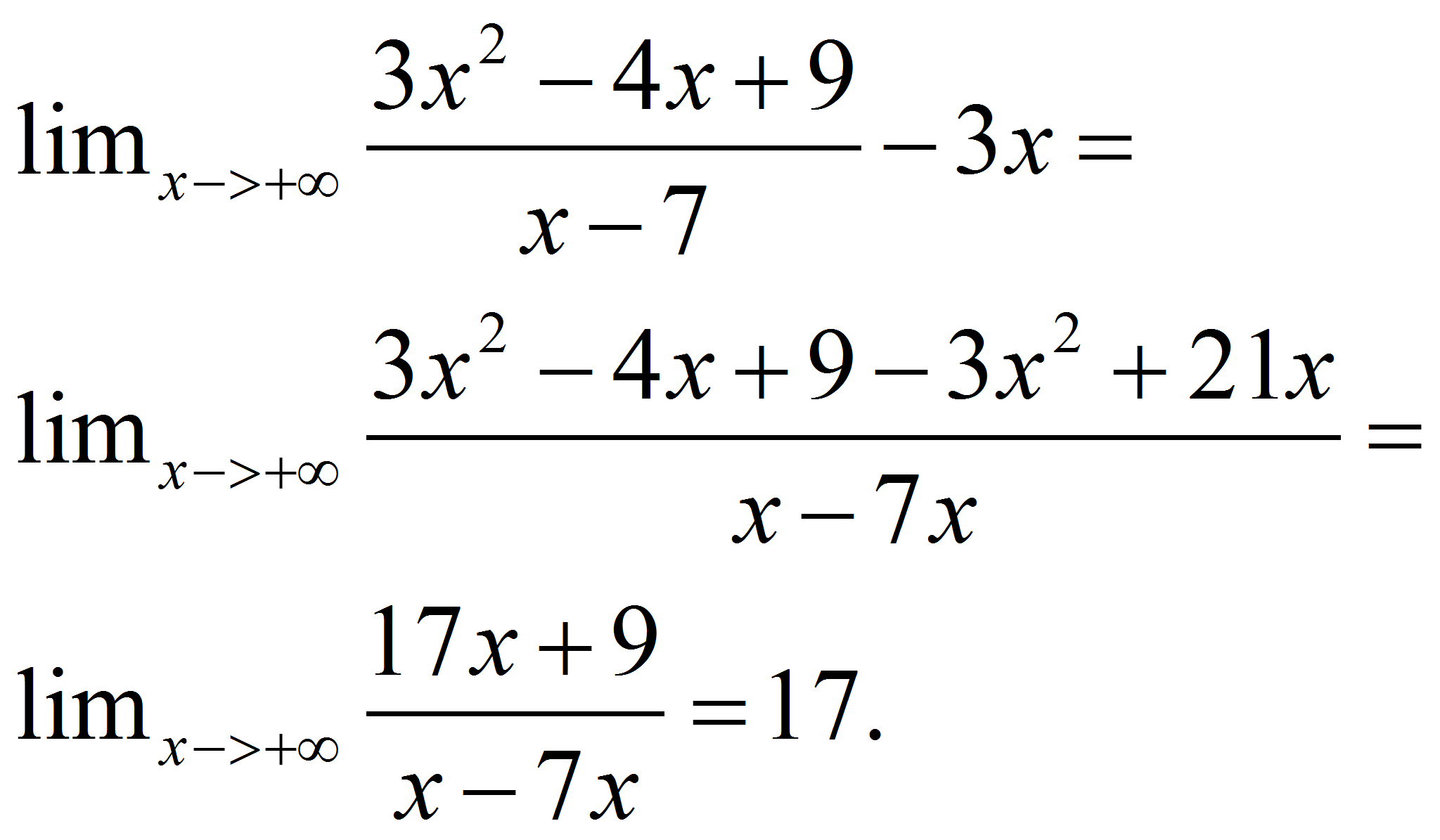
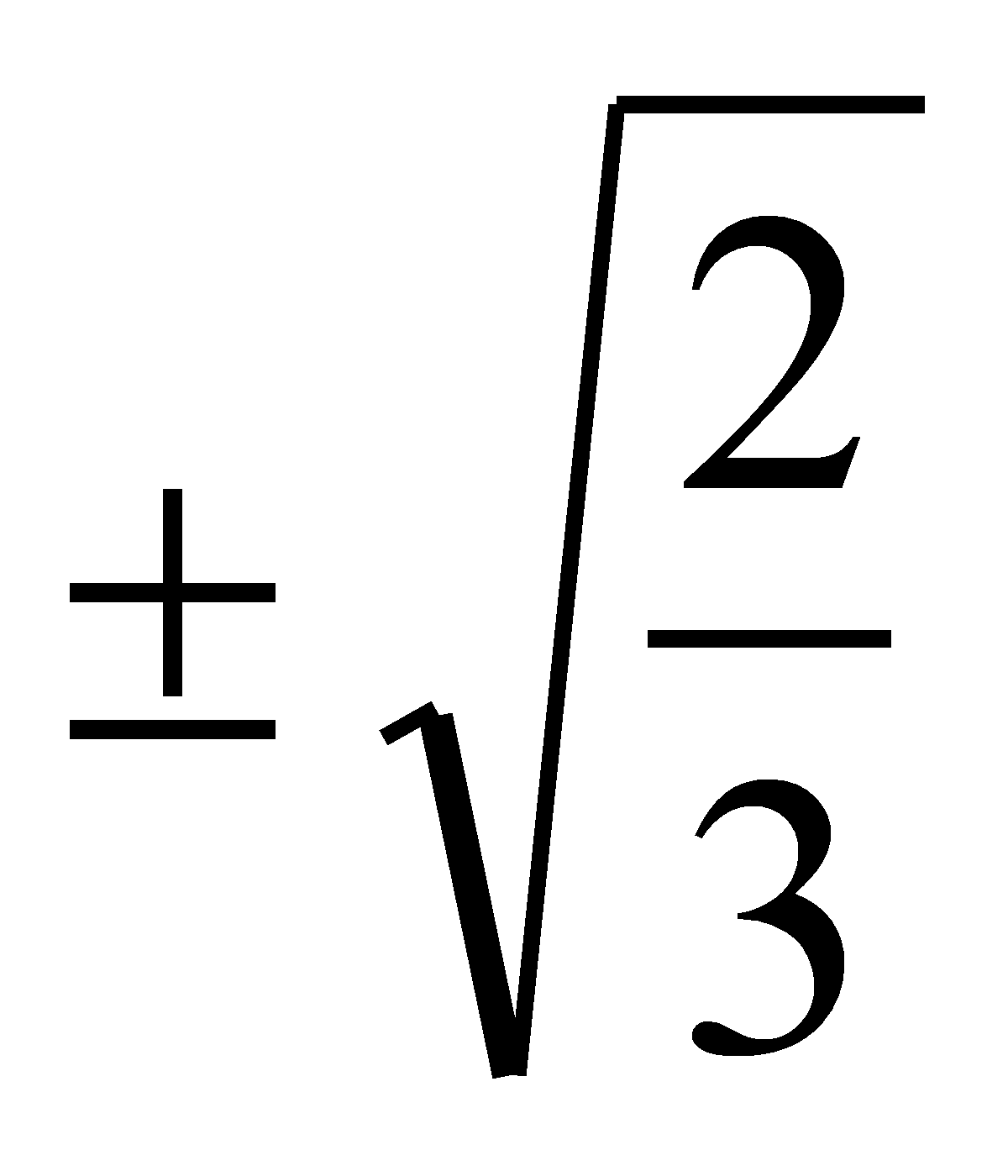 son las raíces de la derivada
segunda.
son las raíces de la derivada
segunda. 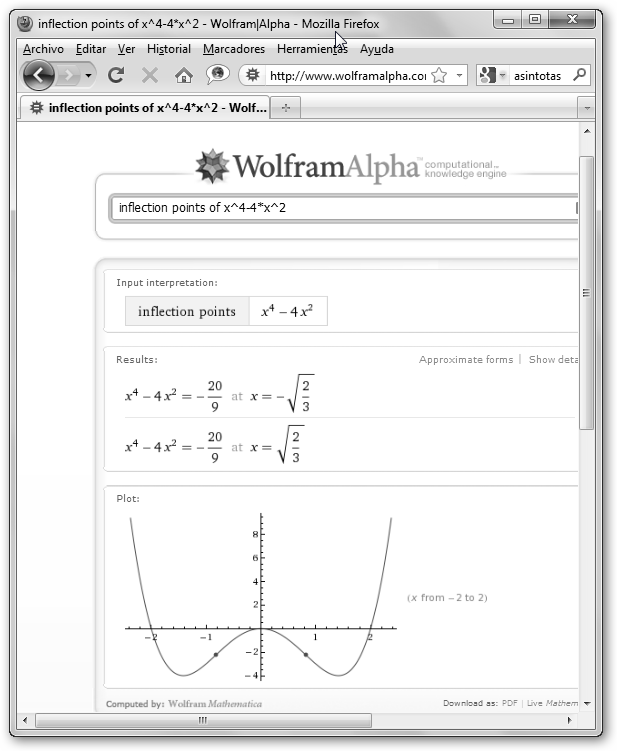
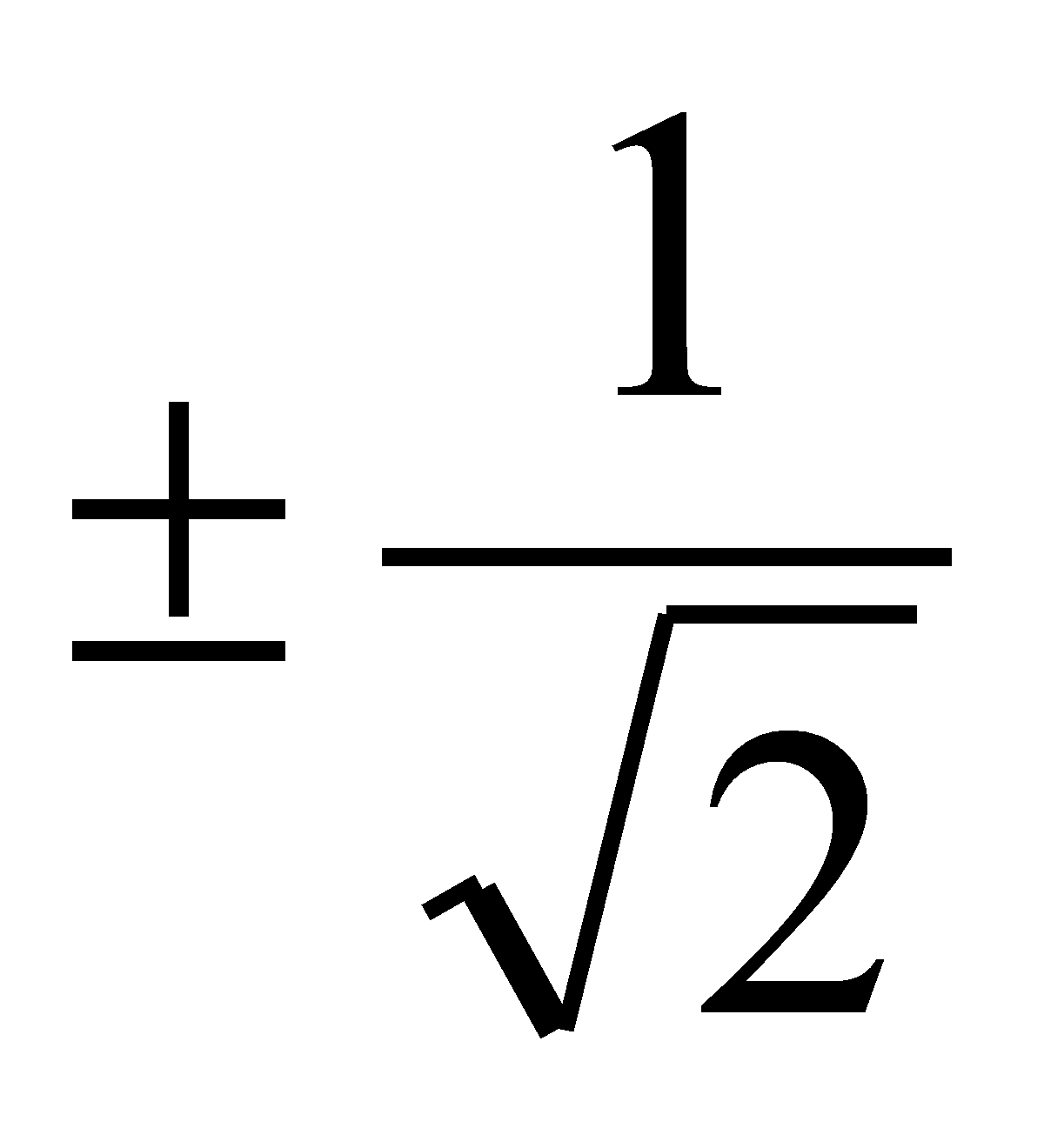 .
.
 .
.
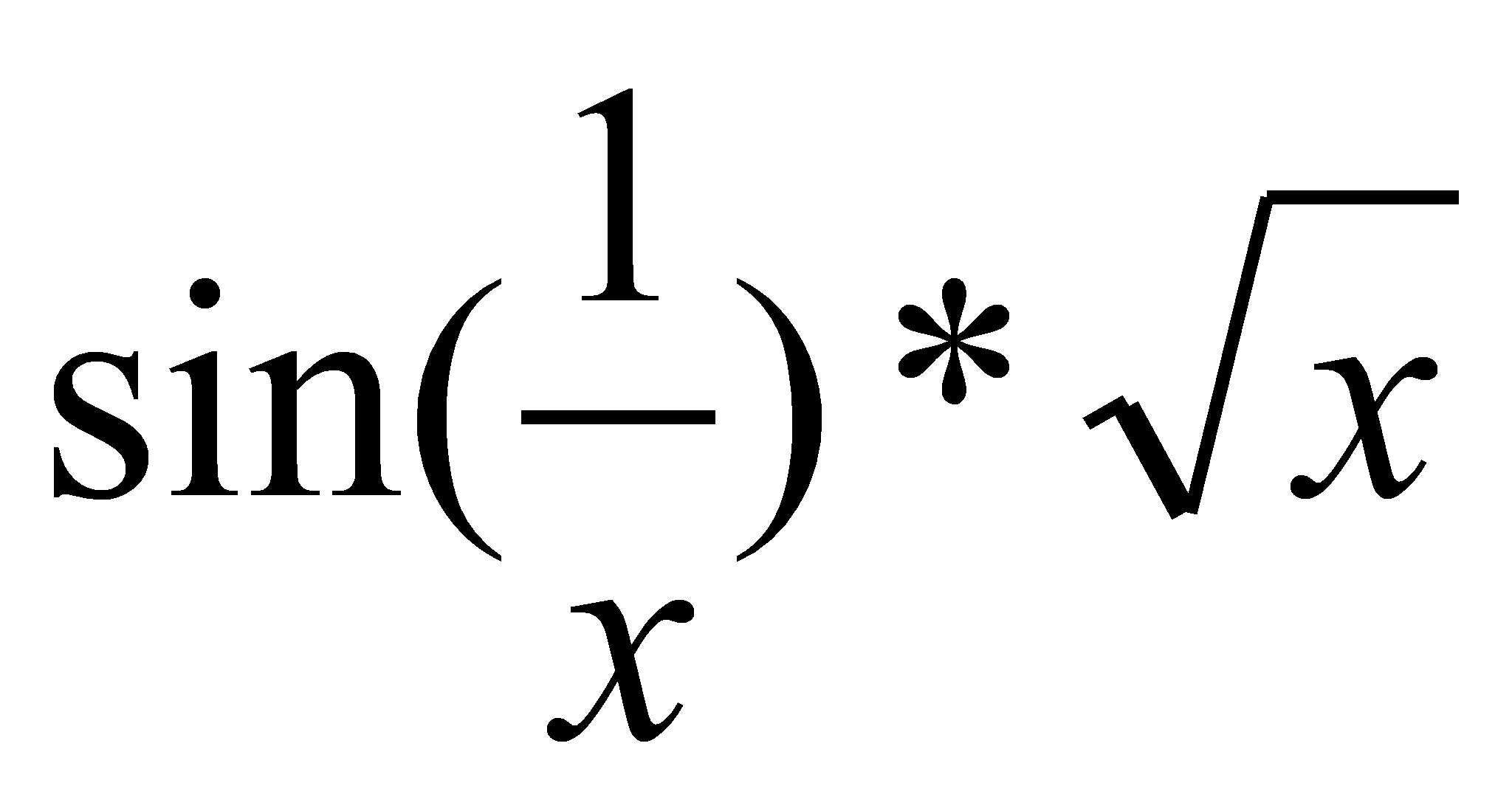 , escribe plot(función) o plot función.
, escribe plot(función) o plot función.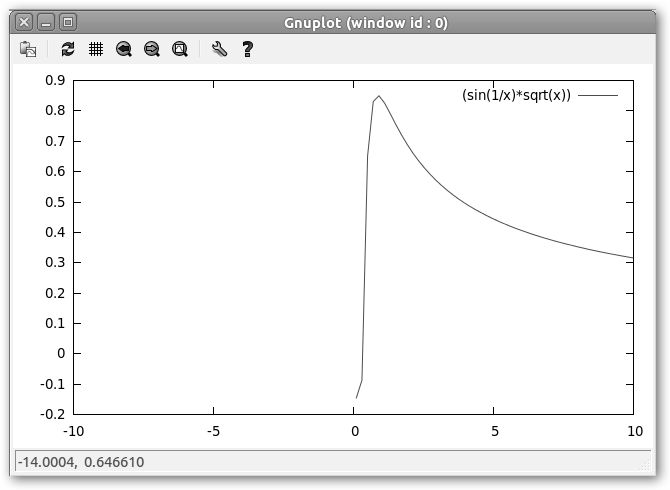
 :
:
 ?
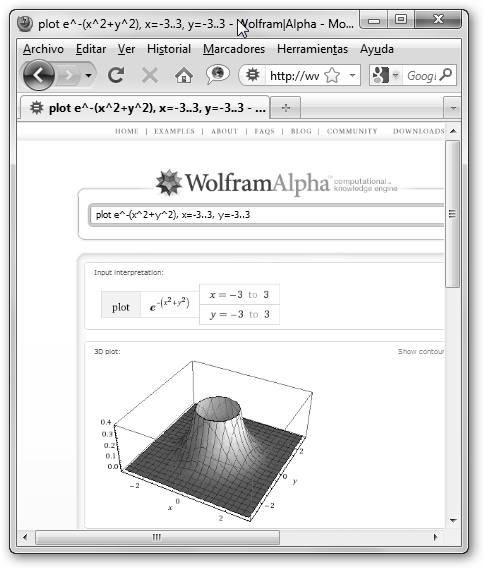
Escribe en WolframAlpha la siguiente línea: plot
e^-(x^2+y^2), x=-3..3, y=-3..3.
?
Escribe en WolframAlpha la siguiente línea: plot
e^-(x^2+y^2), x=-3..3, y=-3..3.