
|
 |
 |
|
 |
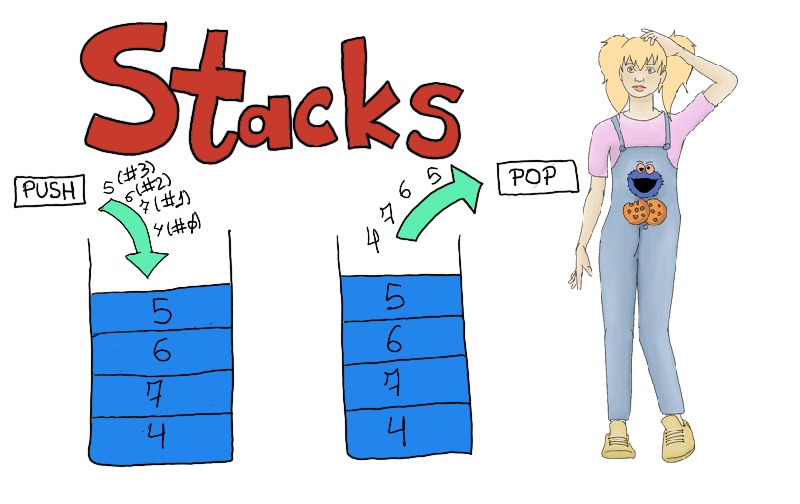
A stack is a data structure used to store a collection of objects or elements where the addition of new items and the removal of existing items always take place at the top of the stack.
class Stack(object):
def __init__(self):
self.items = []
def __len__(self): # It returns the number of elements in the stack.
return len(self.items)
def push(self, item): # It adds a new item to the top of the stack.
self.items.append(item)
The top of the stack is the last element in our list. However, the intricacies of our implementation are totally hidden from the user.
def pop(self): # It removes the top element from the stack and returns the removed item.
if not self.is_empty():
return self.items.pop() # The Python's pop() method takes a single argument (index). If an argument is not passed to the function, it uses the default index -1.
def peek(self): # It returns the top element from the stack but does not remove it.
if not self.is_empty():
return self.items[-1]
def is_empty(self): # It returns true when the stack is empty, otherwise, the method returns false.
return len(self.items) == 0
def __str__(self): # It allows us to print our stack.
s = "{ "
for i in range(len(self.items)):
if i != len(self.items)-1:
s += str(self.items[i]) + ", "
else:
s += str(self.items[i]) + " }"
return s
@classmethod
def createRandomStack(cls, n):
myStack = Stack()
for i in range(n):
i = random.randint(0, 100)
myStack.push(i)
return myStack
def main():
myStack = Stack.createRandomStack(10)
print(myStack) # { 58, 8, 91, 52, 98, 30, 41, 4, 32, 37 }
print(len(myStack)) # 10
print(myStack.pop()) # 37
print(myStack) # { 58, 8, 91, 52, 98, 30, 41, 4, 32 }
if __name__ == '__main__':
main()
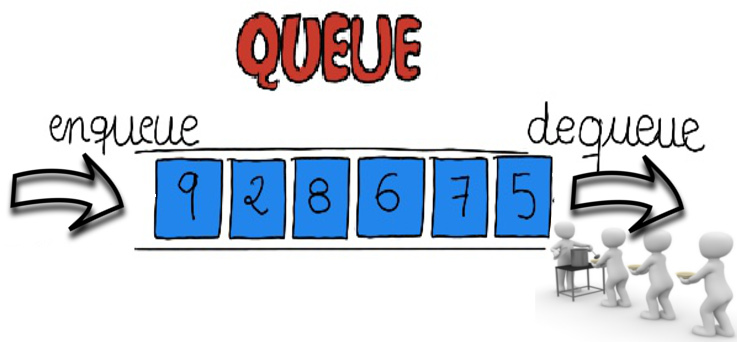
A queue is a data structure used to store a collection of objects or elements which works exactly like how a real-life queue works, that is, a FIFO data structure in which the element that is inserted first into the queue is the first one to be taken out. It models or enforces a first-come first-serve policy.
class Queue():
def __init__(self):
self.items = []
def __len__(self): # It returns the number of elements in the queue.
return len(self.items)
def enqueue(self, item): # It adds a new item to the tail of the queue. _The tail of the queue is the first element in our list.
self.items.insert(0, item)
def dequeue(self): # It removes the first element from the queue (the element at the head of the queue) and returns the removed item.
if not self.is_empty():
return self.items.pop()
def is_empty(self): # It returns true when the queue is empty, otherwise, the method returns false.
return len(self.items) == 0
def peek(self): # It returns the first element from the queue but does not remove it.
if not self.is_empty():
return self.items[-1]
def __str__(self): # It allows us to print our queue.
s = "{ "
for i in range(len(self.items)):
if i != len(self.items)-1:
s += str(self.items[i]) + ", "
else:
s += str(self.items[i]) + " }"
return s
@classmethod
def createRandomQueue(cls, n):
myQueue = Queue()
for i in range(n):
i = random.randint(0, 100)
myQueue.enqueue(i)
return myQueue
def main():
myQueue = Queue.createRandomQueue(10)
print(myQueue) # { 76, 2, 15, 58, 60, 1, 30, 77, 35, 7 }
print(len(myQueue)) # 10
print(myQueue.dequeue()) # 7
print(myQueue) # { 76, 2, 15, 58, 60, 1, 30, 77, 35 }
if __name__ == '__main__':
main()
In real life, a queue is a line of customers waiting for a service of some kind. In most cases, the first customer in line (the first one to arrive) is the first one to be served. In airports, priority queues are now visible everywhere. Many airlines now board their passengers according to the amount of money they’ve paid for their tickets.
Each customer or patient is assigned a priority when first entering the store, the waiting queue of the emergency service, etc., and the one with the highest priority goes first, regardless of the order of arrival. That is, he or she will get into line ahead of all people with lower priority and behind everyone with an equal or higher priority.
import doctest
import heapq
import random
from heapq import heappush, heappop
from copy import deepcopy
class PriorityQueue:
""" It implements a priority queue.
A priority queue sorts and dequeues elements based on their priorities.
Args:
heap : It uses the heap data structure provided by heapq to create a priority queue.
The smallest element will be popped out the first from the queue regardless of the order in which the elements were queued.
"""
def __init__(self):
self.heap = []
def push(self, e):
"""
It inserts a new element 'e'.
>>> myQueue = PriorityQueue.createFromList([12, 9, 3, 14, 29, 4, 5, 13, 18])
>>> myQueue.push(7)
>>> print(myQueue)
{ 3 4 5 7 9 12 13 14 18 29 }
"""
heappush(self.heap, e) # heappush insert the element e into the heap, _but the order is adjusted to maintain the heap properties_.
def pop(self):
"""
It removes the minimum element from the queue.
>>> PriorityQueue.createFromList([12, 9, 3, 14, 9, 4, 5, 13, 18]).pop()
3
"""
return heappop(self.heap) # heappop removes the smallest element from the heap, _but the order is adjusted to maintain the heap properties_.
def is_empty(self):
"""
It returns true when the queue is empty; otherwise, the method returns false.
>>> PriorityQueue.createFromList([12, 9, 3, 14, 9, 4, 5, 13, 18]).is_empty()
False
>>> PriorityQueue.createFromList([]).is_empty()
True
"""
return len(self.heap)==0
def __len__(self):
"""
It returns the number of elements in the priority queue.
>>> len(PriorityQueue.createFromList([12, 9, 3, 14, 29, 4, 5, 13, 18]))
9
"""
return len(self.heap)
def __str__(self):
"""
It allows us to print out our priority queue.
>>> print(PriorityQueue.createFromList([12, 9, 3, 14, 29, 4, 5, 13, 18]))
{ 3 4 5 9 12 13 14 18 29 }
"""
copy = deepcopy(self)
s = "{"
while not copy.is_empty():
s += " " + str(copy.pop())
s += " }"
return s
@classmethod
def createFromList(cls, myList):
"""
It takes as input a list and transforms it into a priority queue.
"""
myPriorityQueue = PriorityQueue()
heapq.heapify(myList) # heapify converts the list into a heap data structure.
myPriorityQueue.heap = myList
return myPriorityQueue
@classmethod
def createRandomPriorityQueue(cls, n):
"""
It creates a priority queue with n random numbers.
"""
myList = [random.randint(1, 20) for i in range(n)]
myPriorityQueue = PriorityQueue()
for i in range(n):
i = random.randint(0, 100)
myPriorityQueue.push(i)
return myPriorityQueue
def main():
myQueue = PriorityQueue.createFromList([12, 9, 3, 14, 29, 4, 5, 13, 18])
print(myQueue)
myQueue.push(7)
print(myQueue)
print(len(myQueue))
print(myQueue.pop())
print(myQueue)
my2Queue = PriorityQueue.createRandomPriorityQueue(7)
print(my2Queue)
if __name__ == '__main__':
doctest.testmod()
main()
[nmaximo7@myarch myPython]$ python priorityQueue.py
{ 3 4 5 9 12 13 14 18 29 }
{ 3 4 5 7 9 12 13 14 18 29 }
10
3
{ 4 5 7 9 12 13 14 18 29 }
{ 8 43 54 66 77 83 94 }
A tree is a nonlinear data structure that’s quite often used to represent hierarchical data. A tree has a value and children, and its children are themselves trees. It is more technically defined as a graph where there is at most one path from any node to any other node.
A binary tree is a tree data structure used to store a collection of objects or elements in which each node has at most two children, which are referred to as the left and the right child.
A binary search tree is a binary tree in which, at any node, all the nodes in the left subtree have a lesser value than the node, and all nodes in the right subtree have a greater value than the node. It quickly allows us to maintain a sorted list of numbers.
class BinaryTree:
def __init__(self, value):
self.data = value
self.left = None
self.right = None
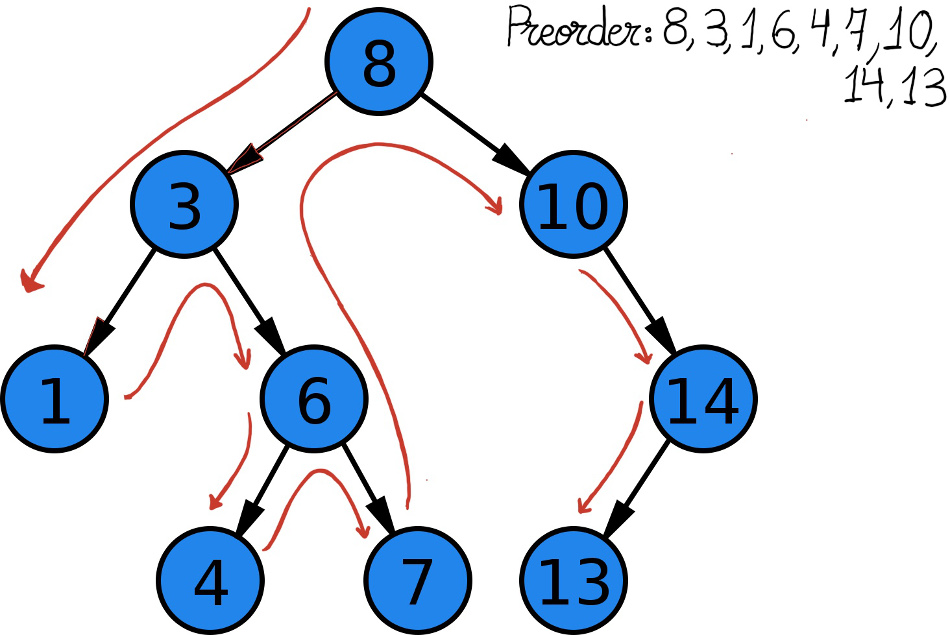
A binary tree is a non-linear data structure, and therefore there is more than one way to traverse through the tree data.
def preorder(self):
"""In a preorder traversal, the root node is visited first, followed by the left tree, then the right tree. [8, 3, 1, 6, 4, 7, 10, 14, 13]"""
result = []
result.append(self.data)
if self.left is not None:
result += self.left.preorder()
if self.right is not None:
result += self.right.preorder()
return result
def inorder(self):
"""In an inorder traversal, the left tree is visited first, followed by the root node, then followed by the right tree."""
result = []
if self.left is not None:
result += self.left.inorder()
result.append(self.data)
if self.right is not None:
result += self.right.inorder()
return result
The inorder traversal produces the sorted list (more technically, the sorted sequence of keys), e.g. [1, 3, 4, 6, 7, 8, 10, 13, 14]
def postorder(self):
"""In a postorder traversal, the left tree is visited first, followed by the right tree, then the root node. [1, 4, 7, 6, 3, 13, 14, 10, 8]"""
result = []
if self.left is not None:
result += self.left.postorder()
if self.right is not None:
result += self.right.postorder()
result.append(self.data)
return result
A level order traversal, i.e. traverse the tree level-by-level, is implemented using a queue. We need to visit the root node first and then visit its child nodes, then their child nodes, etc. First, we push the root inside the queue. Then, we loop till the queue is empty, popping out the first node in the queue and pushing its child nodes inside the queue, e.g. [8, 3, 10, 1, 6, 14, 4, 7, 13]
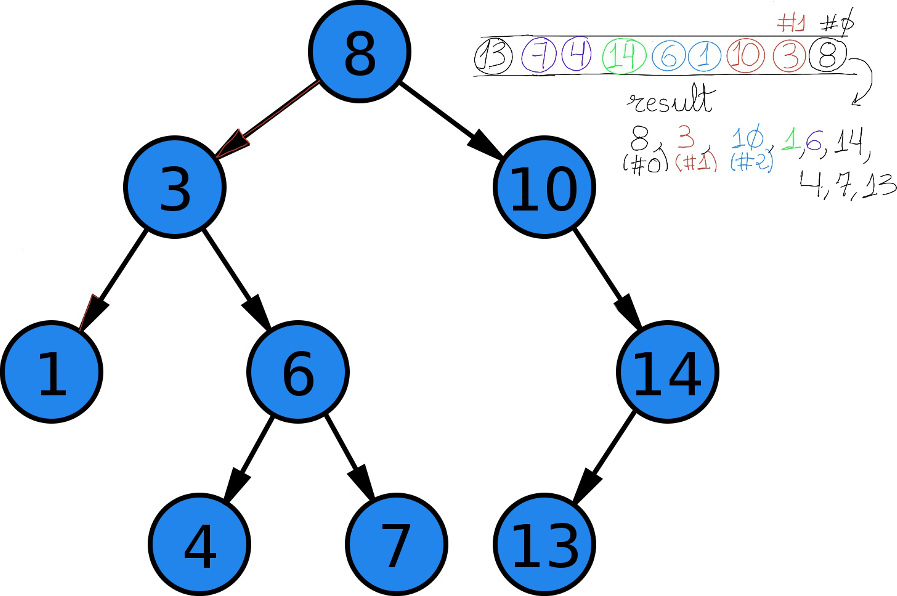
def level(self):
queue = Queue()
queue.enqueue(self)
result = []
while len(queue) > 0:
result.append(queue.peek().data)
myNode = queue.dequeue()
if myNode.left is not None:
queue.enqueue(myNode.left)
if myNode.right is not None:
queue.enqueue(myNode.right)
return result
def __str__(self):
return str(self.level())
Displaying all the nodes in reverse level order is quite similar to a level order traversal, but we use a stack, too. First, we push the root inside the queue. Then, we loop till the queue is empty, popping out the first node in the queue, pushing it into the stack (observe that we use a stack to keep top-level nodes at the bottom of the stack), then pushing its right child first and then its left child into the queue, e.g. [4, 7, 13, 1, 6, 14, 3, 10, 8].
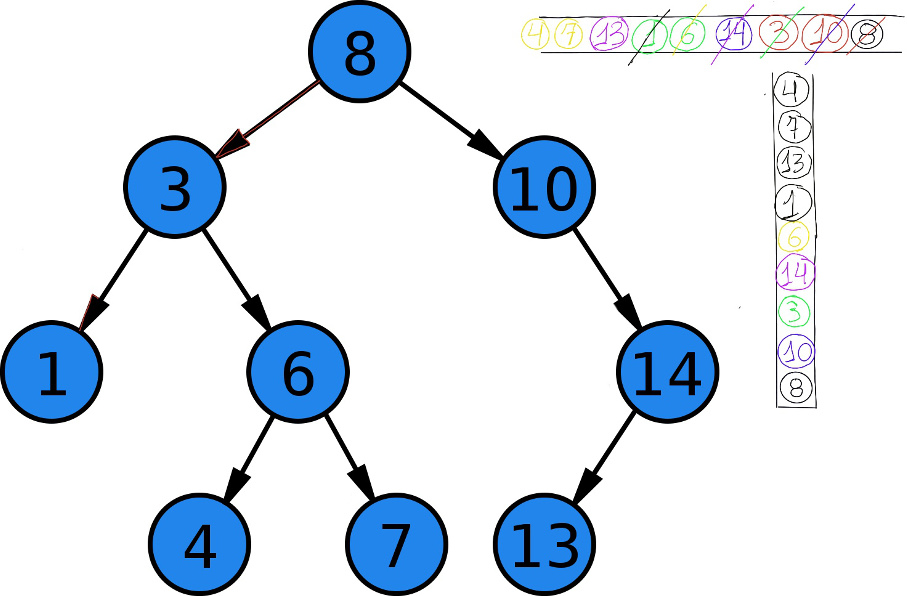
def reverse_level(self):
queue = Queue()
stack = Stack()
queue.enqueue(self)
result = []
while len(queue) > 0:
myNode = queue.dequeue()
stack.push(myNode)
if myNode.right is not None:
queue.enqueue(myNode.right)
if myNode.left is not None:
queue.enqueue(myNode.left)
while len(stack) > 0:
node = stack.pop()
result.append(node.data)
return result
def is_leaf(self): # It returns True if the node does not have any child nodes and returns False otherwise
return (self.left is None) and (self.right is None)
def add_child(self, value): # When looking for a place to insert a new "value", we need to traverse the tree from root to leaf, making comparisons to the values of the tree's nodes and deciding based on these comparisons to continue searching in the left or right subtrees.
if value == self.data:
return
if value < self.data:
if self.left is not None: # We need to continue searching in the left subtree.
self.left.add_child(value)
else: # If value is smaller than the current node's data and the current node does not have any left child, then we have found its place.
self.left = BinaryTree(value)
else:
if self.right is not None:
self.right.add_child(value)
else:
self.right = BinaryTree(value)
@classmethod
def build_tree(cls, values): # It builds a tree from a list representation
myTree = BinaryTree(values[0])
for i in range(1, len(values)):
myTree.add_child(values[i])
return myTree
def print_tree(self, traversal_type):
if traversal_type == "preorder":
return self.preorder()
elif traversal_type == "inorder":
return self.inorder()
elif traversal_type == "postorder":
return self.postorder()
elif traversal_type == "level":
return self.level()
elif traversal_type == "reverse_level":
return self.reverse_level()
else:
print("Traversal type " + str(traversal_type) + " not recognized.")
return False
def height(self): # _The height of a binary tree is the maximum depth of the tree_, that is, the distance from the root node to its furthest leaf.
if self is None:
return 0
if self.is_leaf():
return 1
else:
leftHeight, rightHeight = 0, 0
if self.left is not None:
leftHeight = self.left.height()
if self.right is not None:
rightHeight = self.right.height()
return 1 + max(leftHeight, rightHeight)
def size(self): # The size of a binary tree is the number of nodes in it.
if self is None:
return 0
if self.is_leaf():
return 1
leftSize, rightSize = 0, 0
if self.left is not None:
leftSize = self.left.size()
if self.right is not None:
rightSize = self.right.size()
return 1 + leftSize + rightSize
def find(self, value):
"""To find value, we need to traverse the tree from root to leaf, making comparisons to the values of the tree's nodes and deciding based on these comparisons to continue searching in the left or right subtrees. If the value at the current node is less than the search target, then we need to search to the right, so we recursively proceed down the right subtree, else if it’s greater than the search target, then we will need to go down the left subtree."""
if self is None:
return False
if self.data == value:
return True
elif (value < self.data and self.left is not None):
return self.left.find(value)
elif (value > self.data and self.right is not None):
return self.right.find(value)
else:
return False
def delete(self, value):
"""First, we should proceed the same as before, we need to traverse the tree, making comparisons to the values of the tree's nodes and deciding based on these comparisons to continue searching in the left or right subtrees."""
if value < self.data:
if self.left is not None:
self.left = self.left.delete(value)
elif value > self.data:
if self.right is not None:
self.right = self.right.delete(value)
else: # We have already found it!
if self.is_leaf(): # If the node is a leaf node, we just return None.
return None
elif self.left is None: # If the node does have one single child, say the right child, we return it. In other words, its child takes its position.
return self.right
elif self.right is None:
return self.left
# This is the tricky part, the node has two children. We need to find the minimum value in its right subtree (1), copy its value (2), and remove the duplicate (3).
min_value = self.right.find_min() # (1)
self.data = min_value # (2)
self.right = self.right.delete(min_value) # (3)
return self
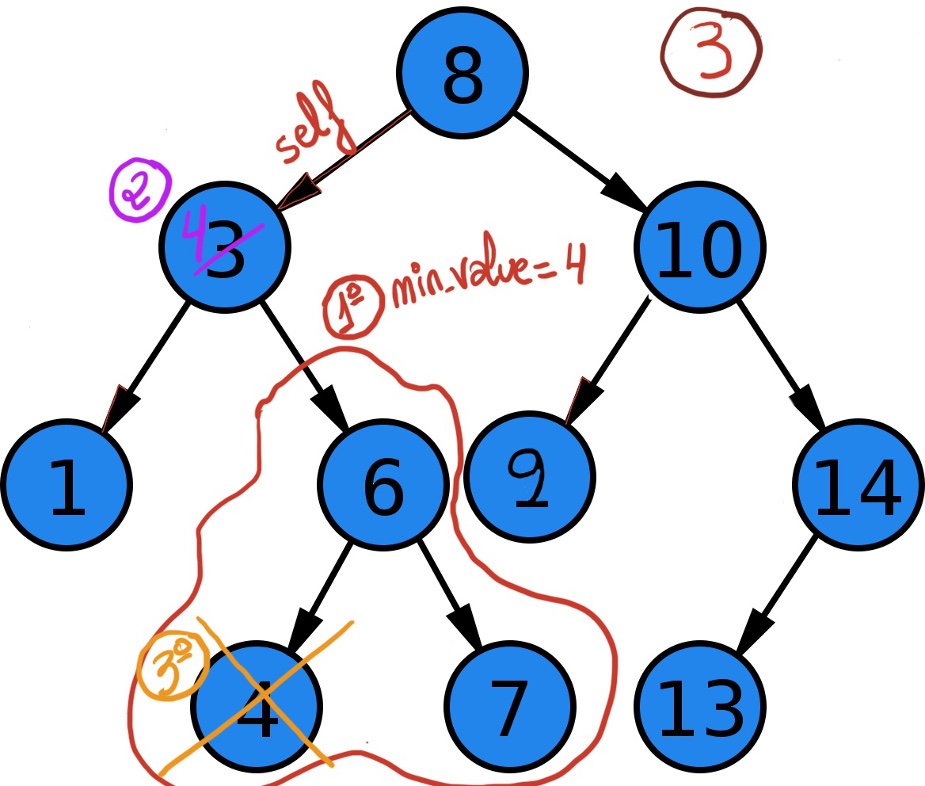
def find_min(self):
if self.left is None:
return self.data
return self.left.find_min()
def main():
tree = BinaryTree.build_tree([8, 3, 10, 1, 6, 14, 4, 7, 13])
print(tree.print_tree("level")) # [8, 3, 10, 1, 6, 14, 4, 7, 13]
print(tree.print_tree("preorder")) # [8, 3, 1, 6, 4, 7, 10, 14, 13]
print(tree.print_tree("inorder")) # [1, 3, 4, 6, 7, 8, 10, 13, 14]
print(tree.print_tree("postorder")) # [1, 4, 7, 6, 3, 13, 14, 10, 8]
print(tree.print_tree("reverse_level")) # [4, 7, 13, 1, 6, 14, 3, 10, 8]
print(tree.height()) # 4
print(tree.size()) # 9
print(tree.find(6)) # True
print(tree.find(13)) # True
print(tree.find(2)) # False
print(tree.find_min()) # 1
print(tree.is_leaf()) # False
tree.delete(7)
tree.delete(3)
print(tree) # [8, 4, 10, 1, 6, 14, 13]
if __name__ == '__main__':
main()
A balanced binary tree is defined as a binary tree in which the left and right subtrees of every node differ in height by no more than 1.
def is_balanced(self):
if self is None:
return True
if self.is_leaf():
return True
if self.right is None:
return self.left.height() <= 1
if self.left is None:
return self.right.height() <= 1
return self.right.is_balanced() and self.left.is_balanced() and abs(self.left.height() - self.right.height()) <= 1
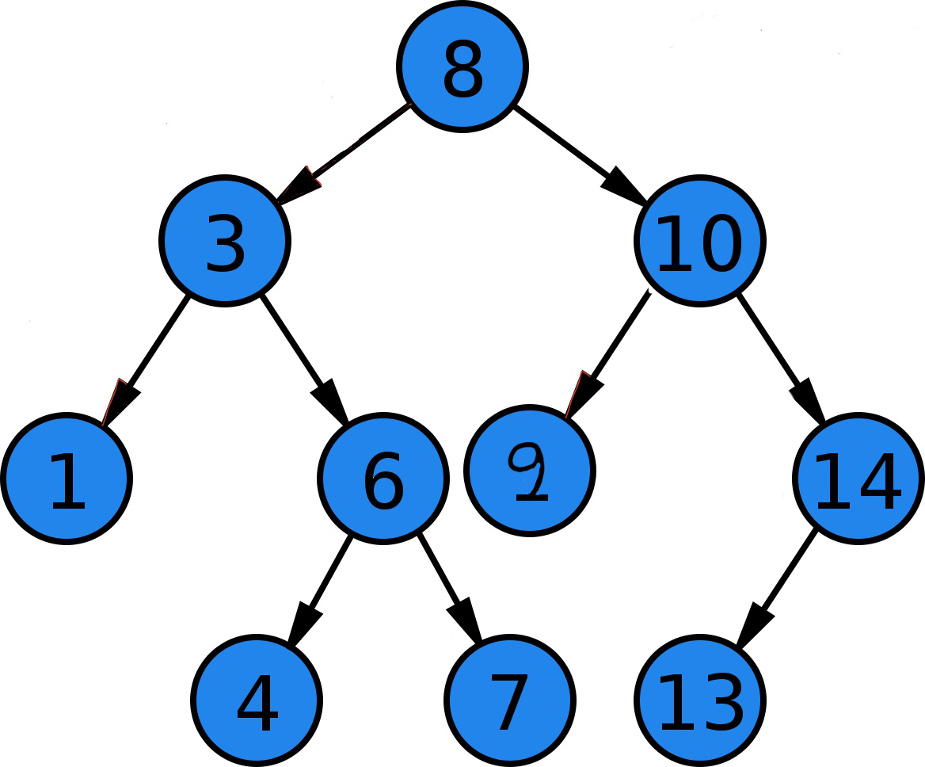
def main():
tree = BinaryTree.build_tree([8, 3, 10, 1, 6, 14, 4, 7, 13]) # [8, 3, 10, 1, 6, 14, 4, 7, 13]
print(tree.is_balanced()) # False
tree.add_child(9) # [8, 3, 10, 1, 6, 9, 14, 4, 7, 13]
print(tree.is_balanced()) # True
if __name__ == '__main__':
main()
An “AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes,” GeeksforGeeks, AVL Tree | Set 1 (Insertion).